


Next: Two-State System
Up: Time-Independent Perturbation Theory
Previous: Introduction
Before commencing our investigation, it is helpful to introduce some
improved notation. Let the 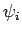 be a complete set of eigenstates
of the Hamiltonian,
be a complete set of eigenstates
of the Hamiltonian,  , corresponding to the eigenvalues
, corresponding to the eigenvalues 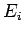 :
i.e.,
:
i.e.,
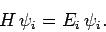 |
(855) |
Now, we expect the 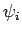 to be orthonormal (see Sect. 4.9).
In one dimension, this implies that
to be orthonormal (see Sect. 4.9).
In one dimension, this implies that
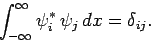 |
(856) |
In three dimensions (see Cha. 7), the above expression generalizes to
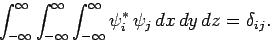 |
(857) |
Finally, if the 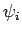 are spinors (see Cha. 10) then
we have
are spinors (see Cha. 10) then
we have
 |
(858) |
The generalization to the case where 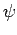 is a product of a regular
wavefunction and a spinor is fairly obvious. We can represent all
of the above possibilities by writing
is a product of a regular
wavefunction and a spinor is fairly obvious. We can represent all
of the above possibilities by writing
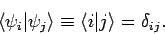 |
(859) |
Here, the term in angle brackets represents the integrals in Eqs. (856)
and (857) in one- and three-dimensional regular space, respectively,
and the spinor product (858) in spin-space. The advantage of
our new notation is its great generality: i.e., it
can deal with one-dimensional wavefunctions, three-dimensional wavefunctions,
spinors, etc.
Expanding a general wavefunction, 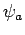 , in terms of the energy
eigenstates,
, in terms of the energy
eigenstates, 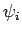 , we obtain
, we obtain
 |
(860) |
In one dimension, the expansion coefficients take the form (see Sect. 4.9)
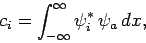 |
(861) |
whereas in three dimensions we get
 |
(862) |
Finally, if 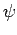 is a spinor then we have
is a spinor then we have
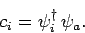 |
(863) |
We can represent all of the above possibilities by
writing
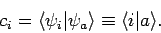 |
(864) |
The expansion (860) thus becomes
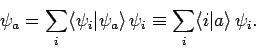 |
(865) |
Incidentally, it follows that
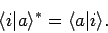 |
(866) |
Finally, if 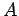 is a general operator, and the wavefunction
is a general operator, and the wavefunction
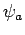 is expanded in the manner shown in Eq. (860), then the expectation value of
is expanded in the manner shown in Eq. (860), then the expectation value of
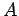 is written (see Sect. 4.9)
is written (see Sect. 4.9)
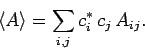 |
(867) |
Here, the 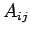 are unsurprisingly known as the matrix
elements of
are unsurprisingly known as the matrix
elements of 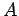 .
In one dimension, the matrix elements take the form
.
In one dimension, the matrix elements take the form
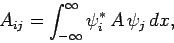 |
(868) |
whereas in three dimensions we get
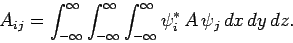 |
(869) |
Finally, if 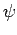 is a spinor then we have
is a spinor then we have
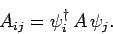 |
(870) |
We can represent all of the above possibilities by
writing
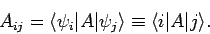 |
(871) |
The expansion (867) thus becomes
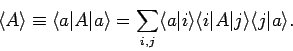 |
(872) |
Incidentally, it follows that [see Eq. (194)]
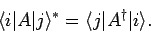 |
(873) |
Finally, it is clear from Eq. (872) that
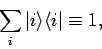 |
(874) |
where the 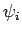 are a complete set of eigenstates, and 1 is the
identity operator.
are a complete set of eigenstates, and 1 is the
identity operator.



Next: Two-State System
Up: Time-Independent Perturbation Theory
Previous: Introduction
Richard Fitzpatrick
2010-07-20
![]() , in terms of the energy
eigenstates,
, in terms of the energy
eigenstates, ![]() , we obtain
, we obtain
![]() is a general operator, and the wavefunction
is a general operator, and the wavefunction
![]() is expanded in the manner shown in Eq. (860), then the expectation value of
is expanded in the manner shown in Eq. (860), then the expectation value of
![]() is written (see Sect. 4.9)
is written (see Sect. 4.9)