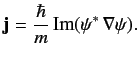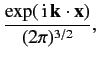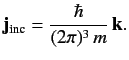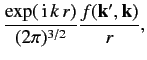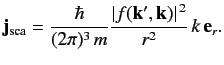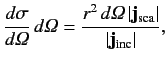Next: Born Approximation
Up: Scattering Theory
Previous: Introduction
Consider time-independent scattering theory, for which the Hamiltonian
of the system is written
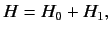 |
(910) |
where 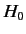 is the Hamiltonian of a free particle of mass
is the Hamiltonian of a free particle of mass  ,
,
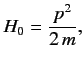 |
(911) |
and 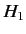 represents the non-time-varying source of the scattering. Let
represents the non-time-varying source of the scattering. Let
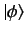 be an energy eigenket of
be an energy eigenket of 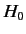 ,
,
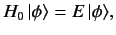 |
(912) |
whose wavefunction
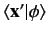 is
is
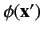 . This state is assumed to be a plane wave state or, possibly, a
spherical wave state.
Schrödinger's equation for the scattering problem is
. This state is assumed to be a plane wave state or, possibly, a
spherical wave state.
Schrödinger's equation for the scattering problem is
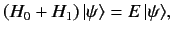 |
(913) |
where
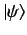 is an energy eigenstate of the total Hamiltonian
whose wavefunction
is an energy eigenstate of the total Hamiltonian
whose wavefunction
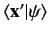 is
is
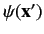 .
In general, both
.
In general, both 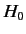 and
and 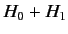 have continuous energy
spectra: i.e., their energy eigenstates are unbound.
We require a solution of Equation (913) that satisfies the
boundary condition
have continuous energy
spectra: i.e., their energy eigenstates are unbound.
We require a solution of Equation (913) that satisfies the
boundary condition
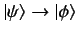 as
as
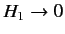 . Here,
. Here,
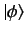 is a solution of the free particle
Schrödinger equation, (912), corresponding to the same energy eigenvalue.
is a solution of the free particle
Schrödinger equation, (912), corresponding to the same energy eigenvalue.
Adopting the Schrödinger representation, we can write the scattering
problem (913) in the form
 |
(914) |
where
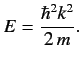 |
(915) |
Equation (914) is called the Helmholtz equation, and can be inverted
using standard Green's function techniques. Thus,
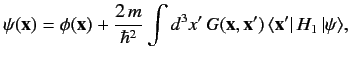 |
(916) |
where
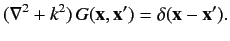 |
(917) |
Note that the solution (916) satisfies the boundary condition
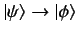 as
as
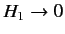 .
As is well-known, the Green's function for the Helmholtz problem is
given by
.
As is well-known, the Green's function for the Helmholtz problem is
given by
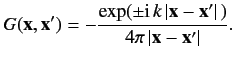 |
(918) |
Thus, Equation (916) becomes
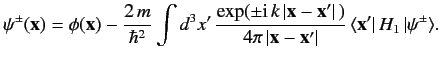 |
(919) |
Let us suppose that the scattering Hamiltonian, 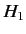 , is only a function
of the position operators. This implies that
, is only a function
of the position operators. This implies that
 |
(920) |
We can write
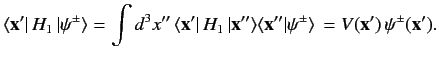 |
(921) |
Thus, the integral equation (919) simplifies to
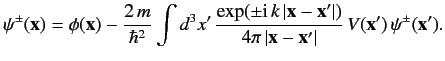 |
(922) |
Suppose that the initial state
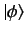 is a plane wave with wavevector
is a plane wave with wavevector 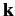 (i.e., a stream of particles of
definite momentum
(i.e., a stream of particles of
definite momentum
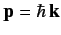 ). The ket corresponding to
this state is denoted
). The ket corresponding to
this state is denoted
 . The associated wavefunction
takes the form
. The associated wavefunction
takes the form
 |
(923) |
The wavefunction is normalized such that
![$\displaystyle \langle {\bf k}\vert{\bf k}'\rangle =\int d^3 x\, \langle {\bf k}...
...\, {\bf x}\cdot({\bf k} -{\bf k}')]} {(2\pi )^3} = \delta ({\bf k} - {\bf k'}).$](img2159.png) |
(924) |
Suppose that the scattering potential
 is only non-zero in some
relatively localized region centered on the origin (
is only non-zero in some
relatively localized region centered on the origin (
 ).
Let us calculate the wavefunction
).
Let us calculate the wavefunction
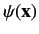 a long way from
the scattering region. In other words, let us adopt the ordering
a long way from
the scattering region. In other words, let us adopt the ordering
 . It is easily demonstrated that
. It is easily demonstrated that
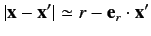 |
(925) |
to first order in 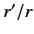 , where
, where
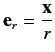 |
(926) |
is a unit vector that points from the scattering region to the
observation point. Here,
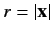 and
and
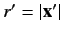 . Let us define
. Let us define
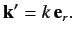 |
(927) |
Clearly, 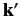 is the wavevector for particles that possess the
same energy as the incoming particles (i.e.,
is the wavevector for particles that possess the
same energy as the incoming particles (i.e., 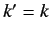 ), but propagate
from the scattering region to the observation point. Note that
), but propagate
from the scattering region to the observation point. Note that
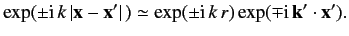 |
(928) |
In the large-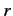 limit, Equation (922) reduces to
limit, Equation (922) reduces to
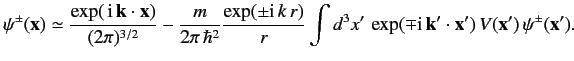 |
(929) |
The first term on the right-hand side is the incident wave. The second term
represents a spherical wave centred on the scattering region. The
plus sign (on 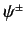 ) corresponds to a wave propagating away from the
scattering region, whereas the minus sign corresponds to a
wave propagating towards the scattering region. It is obvious that
the former represents the physical solution.
Thus, the wavefunction a long way from the scattering region can be
written
) corresponds to a wave propagating away from the
scattering region, whereas the minus sign corresponds to a
wave propagating towards the scattering region. It is obvious that
the former represents the physical solution.
Thus, the wavefunction a long way from the scattering region can be
written
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left[\exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) + \frac{\exp(\,{\rm i}\,k\,r)}{r} f({\bf k}', {\bf k}) \right],$](img2173.png) |
(930) |
where
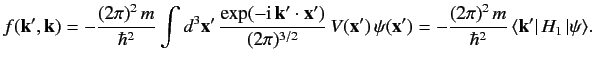 |
(931) |
Let us define the differential cross-section,
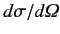 , as
the number of particles per unit time scattered into an element of
solid angle
, as
the number of particles per unit time scattered into an element of
solid angle
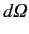 , divided by the incident flux of particles.
Recall, from Chapter 3, that the probability current
(i.e., the particle flux) associated with a
wavefunction
, divided by the incident flux of particles.
Recall, from Chapter 3, that the probability current
(i.e., the particle flux) associated with a
wavefunction 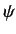 is
is
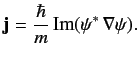 |
(932) |
Thus, the probability flux associated with the incident wavefunction,
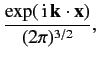 |
(933) |
is
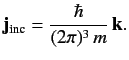 |
(934) |
Likewise, the probability flux associated with the scattered wavefunction,
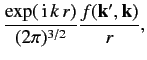 |
(935) |
is
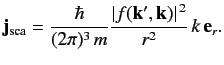 |
(936) |
Now,
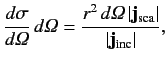 |
(937) |
giving
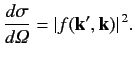 |
(938) |
Thus,
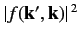 gives the differential cross-section for particles with incident momentum
gives the differential cross-section for particles with incident momentum
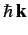 to be scattered
into states whose momentum vectors are directed in a range of solid angles
to be scattered
into states whose momentum vectors are directed in a range of solid angles
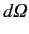 about
about
 . Note that the scattered particles possess
the same energy as the incoming particles (i.e.,
. Note that the scattered particles possess
the same energy as the incoming particles (i.e., 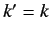 ). This is always
the case for scattering Hamiltonians of the form specified in Equation (920).
). This is always
the case for scattering Hamiltonians of the form specified in Equation (920).



Next: Born Approximation
Up: Scattering Theory
Previous: Introduction
Richard Fitzpatrick
2013-04-08
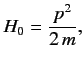
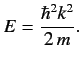
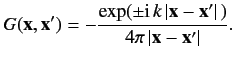
![]() , is only a function
of the position operators. This implies that
, is only a function
of the position operators. This implies that
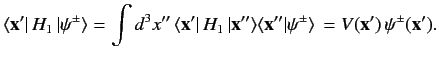
![]() is a plane wave with wavevector
is a plane wave with wavevector ![]() (i.e., a stream of particles of
definite momentum
(i.e., a stream of particles of
definite momentum
![]() ). The ket corresponding to
this state is denoted
). The ket corresponding to
this state is denoted
![]() . The associated wavefunction
takes the form
. The associated wavefunction
takes the form

![$\displaystyle \langle {\bf k}\vert{\bf k}'\rangle =\int d^3 x\, \langle {\bf k}...
...\, {\bf x}\cdot({\bf k} -{\bf k}')]} {(2\pi )^3} = \delta ({\bf k} - {\bf k'}).$](img2159.png)
![]() is only non-zero in some
relatively localized region centered on the origin (
is only non-zero in some
relatively localized region centered on the origin (
![]() ).
Let us calculate the wavefunction
).
Let us calculate the wavefunction
![]() a long way from
the scattering region. In other words, let us adopt the ordering
a long way from
the scattering region. In other words, let us adopt the ordering
![]() . It is easily demonstrated that
. It is easily demonstrated that
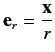
![]() limit, Equation (922) reduces to
limit, Equation (922) reduces to
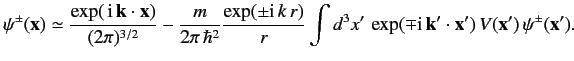
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left[\exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) + \frac{\exp(\,{\rm i}\,k\,r)}{r} f({\bf k}', {\bf k}) \right],$](img2173.png)
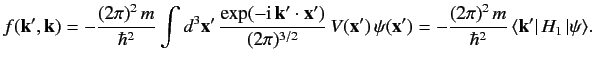
![]() , as
the number of particles per unit time scattered into an element of
solid angle
, as
the number of particles per unit time scattered into an element of
solid angle
![]() , divided by the incident flux of particles.
Recall, from Chapter 3, that the probability current
(i.e., the particle flux) associated with a
wavefunction
, divided by the incident flux of particles.
Recall, from Chapter 3, that the probability current
(i.e., the particle flux) associated with a
wavefunction ![]() is
is