


Next: General Analysis
Up: Time-Dependent Perturbation Theory
Previous: Time-Dependent Perturbation Theory
Suppose that the Hamiltonian of the system under consideration
can be written
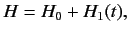 |
(739) |
where 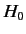 does not contain time explicitly, and
does not contain time explicitly, and 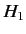 is a small
time-dependent perturbation. It is assumed that we are able to calculate
the eigenkets of the unperturbed Hamiltonian:
is a small
time-dependent perturbation. It is assumed that we are able to calculate
the eigenkets of the unperturbed Hamiltonian:
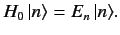 |
(740) |
We know that if the system is in one of the
eigenstates of 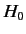 then, in the absence of the external
perturbation, it remains in this state for ever. However,
the presence of a small time-dependent perturbation can, in principle,
give rise to a finite probability that a system initially in some
eigenstate
then, in the absence of the external
perturbation, it remains in this state for ever. However,
the presence of a small time-dependent perturbation can, in principle,
give rise to a finite probability that a system initially in some
eigenstate 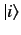 of the unperturbed Hamiltonian
is found in some other eigenstate at a subsequent time (because
of the unperturbed Hamiltonian
is found in some other eigenstate at a subsequent time (because
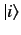 is no longer an exact eigenstate of the total
Hamiltonian).
In other words,
a time-dependent perturbation allows
the system to make transitions between
its unperturbed energy eigenstates. Let us investigate such transitions.
is no longer an exact eigenstate of the total
Hamiltonian).
In other words,
a time-dependent perturbation allows
the system to make transitions between
its unperturbed energy eigenstates. Let us investigate such transitions.
Richard Fitzpatrick
2013-04-08