


Next: Bra Space
Up: Fundamental Concepts
Previous: Fundamental Principles of Quantum
Consider a microscopic system composed of particles, or bodies, with
specific properties (mass, moment of inertia, etc.) interacting according
to specific laws of force. There will be various possible motions of the
particles, or bodies, consistent with these laws of force. Let us term each such
motion a state of the system. According to the principle of superposition
of states, any given state can be regarded as a superposition of two or more other
states. Thus, states must be related to mathematical quantities of a kind that
can be added together to give other quantities of the same kind. The most
obvious examples of such quantities are vectors.
Let us consider a particular microscopic system in a particular state, which we
label 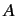 : e.g., a photon with a particular energy, momentum, and polarization.
We can represent this state as a particular vector, which we also
label
: e.g., a photon with a particular energy, momentum, and polarization.
We can represent this state as a particular vector, which we also
label 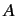 , residing in some vector space, where the other elements of the space
represent all of the other possible states of the system. Such a space
is called a ket space (after Dirac). The state vector
, residing in some vector space, where the other elements of the space
represent all of the other possible states of the system. Such a space
is called a ket space (after Dirac). The state vector 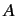 is
conventionally written
is
conventionally written
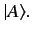 |
(1) |
Suppose that state 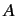 is, in fact, the superposition of two different states,
is, in fact, the superposition of two different states,
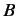 and
and 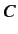 . This interrelation is represented in ket space by writing
. This interrelation is represented in ket space by writing
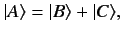 |
(2) |
where 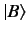 is the vector relating to the state
is the vector relating to the state 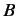 , etc. For instance, state
, etc. For instance, state
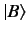 might represent a photon propagating
in the
might represent a photon propagating
in the 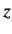 -direction, and plane polarized in the
-direction, and plane polarized in the 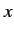 -direction, and state
-direction, and state
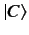 might represent a similar photon plane polarized in the
might represent a similar photon plane polarized in the 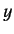 -direction.
In this case,
the sum of these two states represents a photon whose plane of polarization
makes an angle of
-direction.
In this case,
the sum of these two states represents a photon whose plane of polarization
makes an angle of 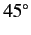 with both the
with both the 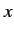 - and
- and 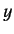 -directions (by analogy
with classical physics). This latter state is represented by
-directions (by analogy
with classical physics). This latter state is represented by
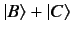 in ket
space.
in ket
space.
Suppose that we want to construct a state whose plane of polarization makes
an arbitrary angle 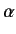 with the
with the 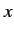 -direction. We can do this
via a suitably weighted superposition of states
-direction. We can do this
via a suitably weighted superposition of states 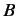 and
and 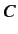 . By analogy
with classical physics, we require
. By analogy
with classical physics, we require
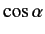 of state
of state 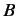 , and
, and
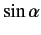 of state
of state 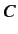 . This new state is represented by
. This new state is represented by
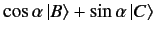 |
(3) |
in ket space. Note that we cannot form a new state by superposing a state
with itself. For instance, a photon polarized in the 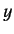 -direction
superposed with another photon polarized in the
-direction
superposed with another photon polarized in the 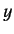 -direction (with the
same energy and momentum) gives
the same photon. This implies
that the ket vector
-direction (with the
same energy and momentum) gives
the same photon. This implies
that the ket vector
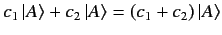 |
(4) |
corresponds to the same state that 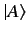 does. Thus, ket vectors differ
from conventional vectors in that their magnitudes, or lengths, are physically
irrelevant. All the states of the system are in one to one correspondence
with all the possible directions of vectors in the ket space, no distinction
being made between the directions of the ket vectors
does. Thus, ket vectors differ
from conventional vectors in that their magnitudes, or lengths, are physically
irrelevant. All the states of the system are in one to one correspondence
with all the possible directions of vectors in the ket space, no distinction
being made between the directions of the ket vectors 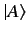 and
and
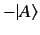 .
There is, however, one caveat to the above statements. If
.
There is, however, one caveat to the above statements. If
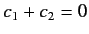 then the
superposition process yields nothing at all: i.e., no state. The absence of
a state is represented by the null vector
then the
superposition process yields nothing at all: i.e., no state. The absence of
a state is represented by the null vector 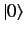 in ket space. The null vector
has the fairly obvious property that
in ket space. The null vector
has the fairly obvious property that
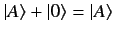 |
(5) |
for any vector 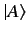 . The fact that ket vectors pointing in the same direction
represent the same state relates ultimately to the quantization of matter: i.e.,
the fact that it comes in irreducible packets called photons, electrons, atoms,
etc.
If we observe a microscopic system then we either see a state
(i.e., a photon, or an atom, or a molecule, etc.) or we see nothing--we can never see
a fraction or a multiple
of a state. In classical physics, if we observe a wave then the amplitude
of the wave can take any value between zero and infinity. Thus, if we were to
represent a classical wave by a vector then the magnitude, or length, of the
vector would correspond to the amplitude of the wave, and the direction
would correspond to the frequency and wavelength,
so that two vectors
of different lengths pointing
in the same direction would represent different wave states.
. The fact that ket vectors pointing in the same direction
represent the same state relates ultimately to the quantization of matter: i.e.,
the fact that it comes in irreducible packets called photons, electrons, atoms,
etc.
If we observe a microscopic system then we either see a state
(i.e., a photon, or an atom, or a molecule, etc.) or we see nothing--we can never see
a fraction or a multiple
of a state. In classical physics, if we observe a wave then the amplitude
of the wave can take any value between zero and infinity. Thus, if we were to
represent a classical wave by a vector then the magnitude, or length, of the
vector would correspond to the amplitude of the wave, and the direction
would correspond to the frequency and wavelength,
so that two vectors
of different lengths pointing
in the same direction would represent different wave states.
We have seen, in Equation (3),
that any plane polarized state of a photon can be represented
as a linear superposition of two orthogonal polarization states
in which the weights are real numbers. Suppose that
we want to construct a circularly polarized photon state. Well, we know from
classical physics that a circularly polarized wave is a superposition of two
waves of equal amplitude, plane polarized in orthogonal directions,
which oscillate in phase quadrature. This suggests that a circularly polarized photon
is the superposition of a photon polarized in the 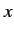 -direction (state
-direction (state 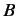 )
and a photon polarized in the
)
and a photon polarized in the 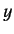 -direction (state
-direction (state 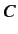 ), with equal weights given
to the two states, but with the proviso that state
), with equal weights given
to the two states, but with the proviso that state 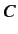 oscillates
oscillates  out of phase
with state
out of phase
with state 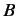 . By analogy with classical physics, we can use complex numbers
to simultaneously represent the weighting and relative phase in a
linear superposition. Thus, a circularly polarized photon is represented by
. By analogy with classical physics, we can use complex numbers
to simultaneously represent the weighting and relative phase in a
linear superposition. Thus, a circularly polarized photon is represented by
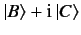 |
(6) |
in ket space. A general elliptically polarized photon is represented by
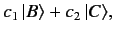 |
(7) |
where 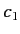 and
and 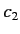 are complex numbers. We conclude that
a ket space
must be a complex vector space if it is to properly
represent the mutual interrelations
between the possible states of a microscopic system.
are complex numbers. We conclude that
a ket space
must be a complex vector space if it is to properly
represent the mutual interrelations
between the possible states of a microscopic system.
Suppose that the ket 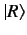 is expressible linearly in terms of the kets
is expressible linearly in terms of the kets
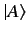 and
and 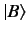 , so that
, so that
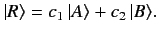 |
(8) |
We say that 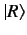 is dependent on
is dependent on 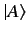 and
and 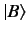 . It follows that
the state
. It follows that
the state 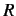 can be regarded as a linear superposition of
the states
can be regarded as a linear superposition of
the states 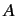 and
and 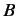 .
So, we can also say that state
.
So, we can also say that state 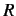 is dependent on states
is dependent on states 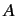 and
and 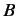 .
In fact, any ket vector (or state) that is expressible linearly in
terms of certain others is said to be dependent on them. Likewise, a
set of ket vectors (or states) are termed independent if none of
them are expressible linearly in terms of the others.
.
In fact, any ket vector (or state) that is expressible linearly in
terms of certain others is said to be dependent on them. Likewise, a
set of ket vectors (or states) are termed independent if none of
them are expressible linearly in terms of the others.
The dimensionality of a conventional vector space is defined as the number
of independent vectors contained in that space. Likewise, the dimensionality
of a ket space is equivalent to the number of independent ket vectors it contains.
Thus, the ket space that represents the possible polarization
states of a photon propagating in the 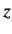 -direction is two-dimensional
(the two independent vectors correspond to photons plane polarized in the
-direction is two-dimensional
(the two independent vectors correspond to photons plane polarized in the
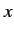 - and
- and 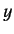 -directions, respectively). Some microscopic
systems have a finite number of independent states (e.g., the spin states
of an electron in a magnetic field). If there are
-directions, respectively). Some microscopic
systems have a finite number of independent states (e.g., the spin states
of an electron in a magnetic field). If there are 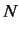 independent states
then the possible states of the
system are represented as an
independent states
then the possible states of the
system are represented as an 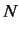 -dimensional ket space. Some microscopic
systems have a denumerably infinite number of independent states (e.g.,
a particle in an infinitely deep, one-dimensional, potential well).
The possible states of such a system are represented as a ket space whose
dimensions are denumerably infinite. Such a space can be treated in more or
less the same manner as a finite-dimensional space. Unfortunately, some
microscopic systems have a nondenumerably infinite number of independent states
(e.g., a free particle). The possible states of such a system are represented
as a ket space whose dimensions are nondenumerably infinite. This type of
space requires a slightly different treatment to spaces of finite, or
denumerably infinite, dimensions (see Section 1.15).
-dimensional ket space. Some microscopic
systems have a denumerably infinite number of independent states (e.g.,
a particle in an infinitely deep, one-dimensional, potential well).
The possible states of such a system are represented as a ket space whose
dimensions are denumerably infinite. Such a space can be treated in more or
less the same manner as a finite-dimensional space. Unfortunately, some
microscopic systems have a nondenumerably infinite number of independent states
(e.g., a free particle). The possible states of such a system are represented
as a ket space whose dimensions are nondenumerably infinite. This type of
space requires a slightly different treatment to spaces of finite, or
denumerably infinite, dimensions (see Section 1.15).
In conclusion, the states of a general microscopic system can be represented
as a complex vector space of (possibly) infinite dimensions. Such a space
is termed a Hilbert space by mathematicians.



Next: Bra Space
Up: Fundamental Concepts
Previous: Fundamental Principles of Quantum
Richard Fitzpatrick
2013-04-08
![]() : e.g., a photon with a particular energy, momentum, and polarization.
We can represent this state as a particular vector, which we also
label
: e.g., a photon with a particular energy, momentum, and polarization.
We can represent this state as a particular vector, which we also
label ![]() , residing in some vector space, where the other elements of the space
represent all of the other possible states of the system. Such a space
is called a ket space (after Dirac). The state vector
, residing in some vector space, where the other elements of the space
represent all of the other possible states of the system. Such a space
is called a ket space (after Dirac). The state vector ![]() is
conventionally written
is
conventionally written
![]() with the
with the ![]() -direction. We can do this
via a suitably weighted superposition of states
-direction. We can do this
via a suitably weighted superposition of states ![]() and
and ![]() . By analogy
with classical physics, we require
. By analogy
with classical physics, we require
![]() of state
of state ![]() , and
, and
![]() of state
of state ![]() . This new state is represented by
. This new state is represented by
![]() -direction (state
-direction (state ![]() )
and a photon polarized in the
)
and a photon polarized in the ![]() -direction (state
-direction (state ![]() ), with equal weights given
to the two states, but with the proviso that state
), with equal weights given
to the two states, but with the proviso that state ![]() oscillates
oscillates ![]() out of phase
with state
out of phase
with state ![]() . By analogy with classical physics, we can use complex numbers
to simultaneously represent the weighting and relative phase in a
linear superposition. Thus, a circularly polarized photon is represented by
. By analogy with classical physics, we can use complex numbers
to simultaneously represent the weighting and relative phase in a
linear superposition. Thus, a circularly polarized photon is represented by
![]() is expressible linearly in terms of the kets
is expressible linearly in terms of the kets
![]() and
and ![]() , so that
, so that
![]() -direction is two-dimensional
(the two independent vectors correspond to photons plane polarized in the
-direction is two-dimensional
(the two independent vectors correspond to photons plane polarized in the
![]() - and
- and ![]() -directions, respectively). Some microscopic
systems have a finite number of independent states (e.g., the spin states
of an electron in a magnetic field). If there are
-directions, respectively). Some microscopic
systems have a finite number of independent states (e.g., the spin states
of an electron in a magnetic field). If there are ![]() independent states
then the possible states of the
system are represented as an
independent states
then the possible states of the
system are represented as an ![]() -dimensional ket space. Some microscopic
systems have a denumerably infinite number of independent states (e.g.,
a particle in an infinitely deep, one-dimensional, potential well).
The possible states of such a system are represented as a ket space whose
dimensions are denumerably infinite. Such a space can be treated in more or
less the same manner as a finite-dimensional space. Unfortunately, some
microscopic systems have a nondenumerably infinite number of independent states
(e.g., a free particle). The possible states of such a system are represented
as a ket space whose dimensions are nondenumerably infinite. This type of
space requires a slightly different treatment to spaces of finite, or
denumerably infinite, dimensions (see Section 1.15).
-dimensional ket space. Some microscopic
systems have a denumerably infinite number of independent states (e.g.,
a particle in an infinitely deep, one-dimensional, potential well).
The possible states of such a system are represented as a ket space whose
dimensions are denumerably infinite. Such a space can be treated in more or
less the same manner as a finite-dimensional space. Unfortunately, some
microscopic systems have a nondenumerably infinite number of independent states
(e.g., a free particle). The possible states of such a system are represented
as a ket space whose dimensions are nondenumerably infinite. This type of
space requires a slightly different treatment to spaces of finite, or
denumerably infinite, dimensions (see Section 1.15).