


Next: Observables
Up: Fundamental Concepts
Previous: Outer Product
Eigenvalues and Eigenvectors
In general, the ket
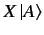 is not a constant multiple of
is not a constant multiple of 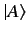 .
However, there are some special kets
known as the eigenkets of operator
.
However, there are some special kets
known as the eigenkets of operator 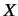 . These are denoted
. These are denoted
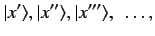 |
(42) |
and have the property
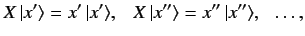 |
(43) |
where  ,
, 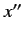 ,
, 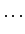 are numbers called
eigenvalues. Clearly, applying
are numbers called
eigenvalues. Clearly, applying 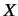 to one of its
eigenkets yields the same eigenket multiplied by the associated eigenvalue.
to one of its
eigenkets yields the same eigenket multiplied by the associated eigenvalue.
Consider the eigenkets and eigenvalues of a Hermitian operator  . These are
denoted
. These are
denoted
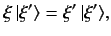 |
(44) |
where
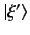 is the eigenket associated with the eigenvalue
is the eigenket associated with the eigenvalue 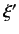 .
Three important results are readily deduced:
.
Three important results are readily deduced:
(i) The eigenvalues are all real numbers, and the eigenkets corresponding
to different eigenvalues are orthogonal.
Since  is Hermitian, the dual equation to Equation (44) (for the eigenvalue
is Hermitian, the dual equation to Equation (44) (for the eigenvalue
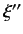 ) reads
) reads
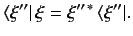 |
(45) |
If we left-multiply Equation (44) by
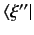 , right-multiply the above
equation by
, right-multiply the above
equation by
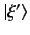 , and take the difference, we obtain
, and take the difference, we obtain
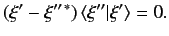 |
(46) |
Suppose that the eigenvalues 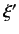 and
and 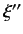 are the same. It follows from the
above that
are the same. It follows from the
above that
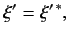 |
(47) |
where we have used the fact that
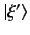 is not the null ket. This proves
that the eigenvalues are real numbers. Suppose that the eigenvalues
is not the null ket. This proves
that the eigenvalues are real numbers. Suppose that the eigenvalues
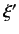 and
and 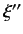 are different. It follows that
are different. It follows that
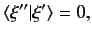 |
(48) |
which demonstrates that eigenkets corresponding to different eigenvalues are
orthogonal.
(ii) The eigenvalues associated with eigenkets are the same as the eigenvalues
associated with eigenbras. An eigenbra of  corresponding to an eigenvalue
corresponding to an eigenvalue
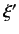 is defined
is defined
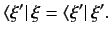 |
(49) |
(iii) The dual of any eigenket is an eigenbra belonging to the same eigenvalue,
and conversely.



Next: Observables
Up: Fundamental Concepts
Previous: Outer Product
Richard Fitzpatrick
2013-04-08
![]() . These are
denoted
. These are
denoted
![]() is Hermitian, the dual equation to Equation (44) (for the eigenvalue
is Hermitian, the dual equation to Equation (44) (for the eigenvalue
![]() ) reads
) reads
![]() corresponding to an eigenvalue
corresponding to an eigenvalue
![]() is defined
is defined