


Next: Observables
Up: Fundamental Concepts
Previous: Outer Product
Eigenvalues and Eigenvectors
In general, the ket
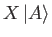 is not a constant multiple of the ket
is not a constant multiple of the ket 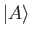 .
However, there are some special kets
known as the eigenkets of operator
.
However, there are some special kets
known as the eigenkets of operator 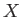 . These are denoted
. These are denoted
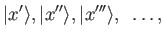 |
(1.45) |
and have the property
where 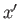 ,
, 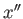 ,
,  ,
, 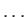 are complex numbers called
eigenvalues. Clearly, applying
are complex numbers called
eigenvalues. Clearly, applying 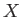 to one of its
eigenkets yields the same eigenket multiplied by the associated eigenvalue.
to one of its
eigenkets yields the same eigenket multiplied by the associated eigenvalue.
Consider the eigenkets and eigenvalues of an Hermitian operator  . These are
denoted
. These are
denoted
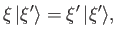 |
(1.47) |
where
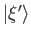 is the eigenket associated with the eigenvalue
is the eigenket associated with the eigenvalue 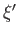 .
Three important results are readily deduced:
.
Three important results are readily deduced:
- The eigenvalues are all real numbers, and the eigenkets corresponding
to different eigenvalues are orthogonal.
Because
 is Hermitian, the dual equation to Equation (1.47) (for the eigenvalue
is Hermitian, the dual equation to Equation (1.47) (for the eigenvalue
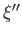 ) reads
) reads
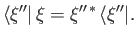 |
(1.48) |
If we left-multiply Equation (1.47) by
 , right-multiply the previous
equation by
, right-multiply the previous
equation by
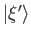 , and take the difference, then we obtain
, and take the difference, then we obtain
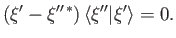 |
(1.49) |
Suppose that the eigenvalues 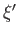 and
and 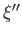 are the same. It follows from the
previous equation that
are the same. It follows from the
previous equation that
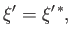 |
(1.50) |
where we have used the fact that
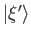 is not the null ket. This proves
that the eigenvalues are real numbers. Suppose that the eigenvalues
is not the null ket. This proves
that the eigenvalues are real numbers. Suppose that the eigenvalues
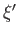 and
and 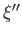 are different. It follows that
are different. It follows that
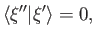 |
(1.51) |
which demonstrates that eigenkets corresponding to different eigenvalues are
orthogonal.
- The eigenvalues associated with eigenkets are the same as the eigenvalues
associated with eigenbras. An eigenbra of
 corresponding to an eigenvalue
corresponding to an eigenvalue
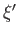 is defined
is defined
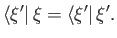 |
(1.52) |
- The dual of any eigenket is an eigenbra belonging to the same eigenvalue,
and conversely.



Next: Observables
Up: Fundamental Concepts
Previous: Outer Product
Richard Fitzpatrick
2016-01-22
![]() . These are
denoted
. These are
denoted