


Next: Time-Independent Perturbation Theory
Up: Addition of Angular Momentum
Previous: Calculation of Clebsch-Gordon Coefficients
- Calculate the Clebsch-Gordon coefficients for adding spin one-half
to spin one.
- An electron in a hydrogen atom occupies the combined spin
and position state whose spinor-wavefunction is
Here, 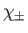 are the eigenstates of
are the eigenstates of 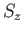 corresponding to the eigenvalues
corresponding to the eigenvalues
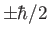 , respectively,
and
, respectively,
and 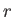 ,
, 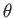 ,
, 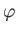 are conventional spherical coordinates.
are conventional spherical coordinates.
- What values would a measurement of
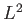 yield, and with
what probabilities?
yield, and with
what probabilities?
- Same for
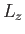 .
.
- Same for
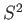 .
.
- Same for
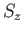 .
.
- Same for
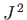 .
.
- Same for
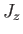 .
.
- What is the probability density for finding the electron at
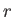 ,
, 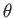 ,
, 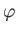 ?
?
- What is the probability density for finding the electron in the
spin-up state (with respect to the
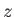 -axis) at radius
-axis) at radius 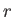 ?
?
[61]
- In a low energy neutron-proton system (with zero orbital angular
momentum) the potential energy is given by
where 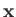 is the vector connecting the two particles,
is the vector connecting the two particles,
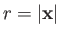 ,
,
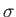
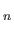 denotes the vector of the Pauli matrices of the neutron,
and
denotes the vector of the Pauli matrices of the neutron,
and
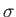
 denotes the vector of the Pauli matrices of the proton. Calculate
the potential energy for the neutron-proton system:
denotes the vector of the Pauli matrices of the proton. Calculate
the potential energy for the neutron-proton system:
- In the spin singlet (i.e., spin zero) state.
- In the spin triplet (i.e., spin one) state.
[Hint: Calculate the expectation value of
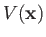 with respect to the overall spin state.] [53]
with respect to the overall spin state.] [53]
- Consider two electrons in a spin singlet (i.e., spin zero) state.
- If a measurement of the spin of one of the electrons shows that it
is in the state with
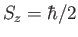 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the 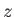 -component of the spin of the
other electron yields
-component of the spin of the
other electron yields
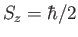 ?
?
- If a measurement of the spin of one of the electrons shows
that it is in the state with
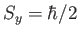 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the  -component of the spin of the
other electron yields
-component of the spin of the
other electron yields
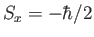 ?
?
- Finally, if electron 1 is in a spin state described by
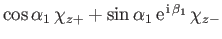 , and
electron 2 is in a spin state described by
, and
electron 2 is in a spin state described by
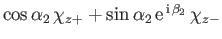 , what is
the probability that the two-electron spin state is a triplet (i.e., spin one) state?
Here,
, what is
the probability that the two-electron spin state is a triplet (i.e., spin one) state?
Here,
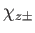 are the eigenstates of
are the eigenstates of 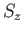 corresponding to the eigenvalues,
corresponding to the eigenvalues,
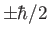 , respectively, for
the electron in question. [53]
, respectively, for
the electron in question. [53]



Next: Time-Independent Perturbation Theory
Up: Addition of Angular Momentum
Previous: Calculation of Clebsch-Gordon Coefficients
Richard Fitzpatrick
2016-01-22
![$\displaystyle \chi(r,\theta,\varphi) = R_{2\,1}(r)\,\left[\sqrt{1/3}\,Y_{1\,0}(\theta,\varphi)\,\chi_+ + \sqrt{2/3}\,Y_{1\,1}(\theta,\varphi)\,\chi_-\right].
$](img1731.png)
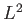 yield, and with
what probabilities?
yield, and with
what probabilities?
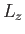 .
.
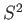 .
.
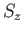 .
.
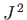 .
.
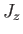 .
.
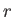 ,
, 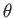 ,
, 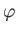 ?
?
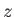 -axis) at radius
-axis) at radius 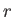 ?
?
![$\displaystyle V({\bf x}) = V_1(r) + V_2(r)\left[3\,\frac{(\mbox{\boldmath $\sig...
...\right] + V_3(r)\,\mbox{\boldmath $\sigma$}_n\cdot\mbox{\boldmath $\sigma$}_p,
$](img1733.png)
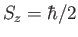 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the 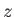 -component of the spin of the
other electron yields
-component of the spin of the
other electron yields
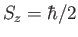 ?
?
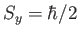 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the  -component of the spin of the
other electron yields
-component of the spin of the
other electron yields
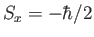 ?
?
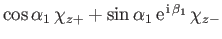 , and
electron 2 is in a spin state described by
, and
electron 2 is in a spin state described by
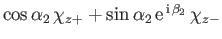 , what is
the probability that the two-electron spin state is a triplet (i.e., spin one) state?
Here,
, what is
the probability that the two-electron spin state is a triplet (i.e., spin one) state?
Here,
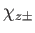 are the eigenstates of
are the eigenstates of 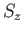 corresponding to the eigenvalues,
corresponding to the eigenvalues,
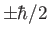 , respectively, for
the electron in question. [53]
, respectively, for
the electron in question. [53]