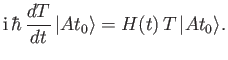Next: Heisenberg Equation of Motion
Up: Quantum Dynamics
Previous: Introduction
Schrödinger Equation of Motion
Consider a system in a state 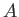 that evolves in time. At time
that evolves in time. At time
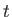 , the state of the system is represented by the ket
, the state of the system is represented by the ket
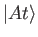 . The label
. The label
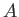 is needed to distinguish this ket from any other ket (
is needed to distinguish this ket from any other ket (
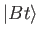 , say)
that is evolving in time. The label
, say)
that is evolving in time. The label 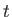 is needed to distinguish the different
states of the system at different times.
is needed to distinguish the different
states of the system at different times.
The final state of the system at time 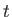 is completely determined by its
initial state at time
is completely determined by its
initial state at time 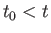 , plus the time interval
, plus the time interval 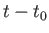 (assuming that
the system is left undisturbed during this time interval). However, the
final state only determines the direction of the final state ket.
Even if we adopt the convention that all state kets have unit norms,
the final ket is still not completely determined, because it can be multiplied
by an arbitrary
phase-factor. However, we expect that if a superposition relation
holds for certain states at time
(assuming that
the system is left undisturbed during this time interval). However, the
final state only determines the direction of the final state ket.
Even if we adopt the convention that all state kets have unit norms,
the final ket is still not completely determined, because it can be multiplied
by an arbitrary
phase-factor. However, we expect that if a superposition relation
holds for certain states at time 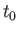 then the same relation
should hold between the corresponding time-evolved states at time
then the same relation
should hold between the corresponding time-evolved states at time 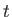 , assuming
that the system is left undisturbed between times
, assuming
that the system is left undisturbed between times 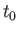 and
and 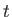 .
In other words,
if
.
In other words,
if
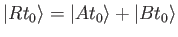 |
(3.1) |
for any three kets then we should have
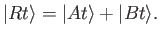 |
(3.2) |
This rule determines the time-evolved kets to within a single arbitrary phase-factor to be multiplied into all of them. The evolved kets cannot be multiplied
by individual phase-factors because this would invalidate the superposition
relation at later times.
According to Equations (3.1) and (3.2), the final ket
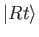 depends linearly
on the initial ket
depends linearly
on the initial ket
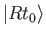 . Thus, the final ket can be regarded as the
result of some linear operator acting on the initial ket: that is,
. Thus, the final ket can be regarded as the
result of some linear operator acting on the initial ket: that is,
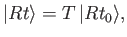 |
(3.3) |
where 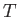 is a linear operator that depends only on the times
is a linear operator that depends only on the times 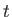 and
and 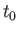 .
The arbitrary phase-factor by which all time-evolved kets may be multiplied
results in
.
The arbitrary phase-factor by which all time-evolved kets may be multiplied
results in 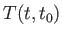 being undetermined to an arbitrary multiplicative constant
of modulus unity.
being undetermined to an arbitrary multiplicative constant
of modulus unity.
Because we have adopted a convention in which the norm of any state ket is unity,
it make sense to define the time evolution operator 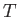 in such a manner that
it preserves the length of any ket upon which it acts
(i.e., if a ket is properly normalized at time
in such a manner that
it preserves the length of any ket upon which it acts
(i.e., if a ket is properly normalized at time 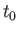 then it will remain normalized at
all subsequent times
then it will remain normalized at
all subsequent times 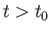 ).
This is always possible,
because the length of a ket possesses no physical significance. Thus,
we require that
).
This is always possible,
because the length of a ket possesses no physical significance. Thus,
we require that
 |
(3.4) |
for any ket 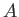 ,
which immediately yields
,
which immediately yields
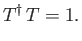 |
(3.5) |
Hence, the time evolution operator 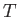 is unitary.
is unitary.
Up to now, the time evolution operator 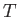 looks very much like the
spatial displacement
operator
looks very much like the
spatial displacement
operator 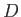 introduced in Section 2.8. However, there are some
important differences between time evolution and spatial displacement. In general,
we do expect the expectation value of a given observable
introduced in Section 2.8. However, there are some
important differences between time evolution and spatial displacement. In general,
we do expect the expectation value of a given observable  to
evolve with time, even if the system is left in a state of undisturbed motion
(after all, time evolution has no meaning unless something observable
changes with time). The triple product
to
evolve with time, even if the system is left in a state of undisturbed motion
(after all, time evolution has no meaning unless something observable
changes with time). The triple product
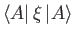 can evolve
either because the ket
can evolve
either because the ket 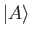 evolves and the operator
evolves and the operator  stays constant,
the ket
stays constant,
the ket 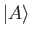 stays constant and the operator
stays constant and the operator  evolves, or both
the ket
evolves, or both
the ket 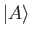 and the operator
and the operator  evolve.
Because we are already committed to evolving state kets, according to Equation (3.3),
let us assume that the time evolution operator
evolve.
Because we are already committed to evolving state kets, according to Equation (3.3),
let us assume that the time evolution operator 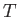 can be chosen in such a
manner that the operators representing the dynamical variables of the
system do not
evolve in time (unless they contain some specific time dependence).
can be chosen in such a
manner that the operators representing the dynamical variables of the
system do not
evolve in time (unless they contain some specific time dependence).
We expect, from physical continuity, that if
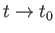 then
then
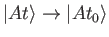 for any ket
for any ket 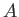 . Thus, the
limit
. Thus, the
limit
 |
(3.6) |
should exist. Note that this limit is simply the derivative of
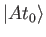 with respect to
with respect to 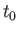 . Let
. Let
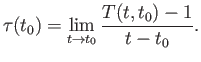 |
(3.7) |
It is easily demonstrated from Equation (3.5) that  is anti-Hermitian:
that is,
is anti-Hermitian:
that is,
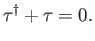 |
(3.8) |
The fact that 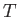 can be replaced by
can be replaced by
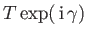 (where
(where 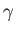 is
real) implies that
is
real) implies that  is undetermined to an arbitrary imaginary additive
constant. (See Section 2.8.) Let us
define the Hermitian operator
is undetermined to an arbitrary imaginary additive
constant. (See Section 2.8.) Let us
define the Hermitian operator
 . This operator is
undetermined to an arbitrary real additive constant. It follows from Equations (3.6)
and (3.7) that
. This operator is
undetermined to an arbitrary real additive constant. It follows from Equations (3.6)
and (3.7) that
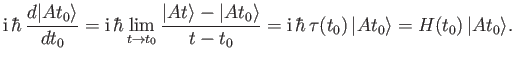 |
(3.9) |
When written for general 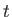 , this equation becomes
, this equation becomes
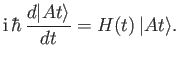 |
(3.10) |
Equation (3.10) gives the general law for the time evolution of a state
ket in a scheme in which the operators representing the dynamical variables remain
fixed. This equation is denoted the Schrödinger equation of motion.
It involves a Hermitian operator 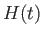 that is, presumably, a characteristic
of the dynamical system under investigation.
that is, presumably, a characteristic
of the dynamical system under investigation.
We saw, in Section 2.8, that
if the operator
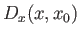 displaces the system along the
displaces the system along the  -axis from
-axis from 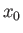 to
to  then
then
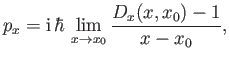 |
(3.11) |
where 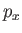 is the operator representing the momentum conjugate to
is the operator representing the momentum conjugate to  . Furthermore, we have
just shown that if the operator
. Furthermore, we have
just shown that if the operator 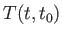 evolves the system in time from
evolves the system in time from 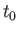 to
to 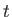 then
then
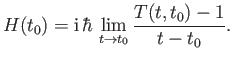 |
(3.12) |
Thus, the
dynamical variable corresponding to
the operator 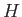 stands to time
stands to time 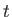 as the momentum
as the momentum 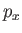 stands to the
coordinate
stands to the
coordinate  . By analogy
with classical physics, this suggests that
. By analogy
with classical physics, this suggests that 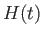 is the operator representing
the total energy of the system. (Recall that, in classical physics,
if the equations of motion of a system are invariant under an
is the operator representing
the total energy of the system. (Recall that, in classical physics,
if the equations of motion of a system are invariant under an  -displacement
then this implies that the system conserves momentum in the
-displacement
then this implies that the system conserves momentum in the
 -direction. Likewise, if the equations of motion are invariant under
a temporal displacement then this implies that the system conserves energy [55].)
The operator
-direction. Likewise, if the equations of motion are invariant under
a temporal displacement then this implies that the system conserves energy [55].)
The operator 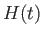 is usually called the Hamiltonian of the system.
The fact that the Hamiltonian is undetermined to an arbitrary real additive
constant is related to the well-known phenomenon that energy is
undetermined to an arbitrary additive constant in physics (i.e., the zero
of potential energy is not well defined).
is usually called the Hamiltonian of the system.
The fact that the Hamiltonian is undetermined to an arbitrary real additive
constant is related to the well-known phenomenon that energy is
undetermined to an arbitrary additive constant in physics (i.e., the zero
of potential energy is not well defined).
Substituting
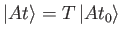 into Equation (3.10) yields
into Equation (3.10) yields
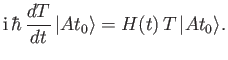 |
(3.13) |
Because this must hold for any initial state
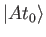 , we conclude that
, we conclude that
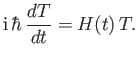 |
(3.14) |
This equation can be integrated to give
![$\displaystyle T(t, t_0) = \exp\left[-\frac{{\rm i}}{\hbar} \int_{t_0}^t dt'\,H(t') \right],$](img622.png) |
(3.15) |
where use has been made of Equations (3.5) and (3.6).
(Here, we assume that Hamiltonian operators
evaluated at different times commute with one another.) The fact that 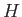 is undetermined to an arbitrary real additive constant leaves
is undetermined to an arbitrary real additive constant leaves
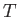 undetermined to a phase-factor. Incidentally, in the previous
analysis, time is not an
operator (we cannot observe time, as such), it is just a parameter (or, more
accurately, a continuous label).
undetermined to a phase-factor. Incidentally, in the previous
analysis, time is not an
operator (we cannot observe time, as such), it is just a parameter (or, more
accurately, a continuous label).



Next: Heisenberg Equation of Motion
Up: Quantum Dynamics
Previous: Introduction
Richard Fitzpatrick
2016-01-22
![]() is completely determined by its
initial state at time
is completely determined by its
initial state at time ![]() , plus the time interval
, plus the time interval ![]() (assuming that
the system is left undisturbed during this time interval). However, the
final state only determines the direction of the final state ket.
Even if we adopt the convention that all state kets have unit norms,
the final ket is still not completely determined, because it can be multiplied
by an arbitrary
phase-factor. However, we expect that if a superposition relation
holds for certain states at time
(assuming that
the system is left undisturbed during this time interval). However, the
final state only determines the direction of the final state ket.
Even if we adopt the convention that all state kets have unit norms,
the final ket is still not completely determined, because it can be multiplied
by an arbitrary
phase-factor. However, we expect that if a superposition relation
holds for certain states at time ![]() then the same relation
should hold between the corresponding time-evolved states at time
then the same relation
should hold between the corresponding time-evolved states at time ![]() , assuming
that the system is left undisturbed between times
, assuming
that the system is left undisturbed between times ![]() and
and ![]() .
In other words,
if
.
In other words,
if
![]() depends linearly
on the initial ket
depends linearly
on the initial ket
![]() . Thus, the final ket can be regarded as the
result of some linear operator acting on the initial ket: that is,
. Thus, the final ket can be regarded as the
result of some linear operator acting on the initial ket: that is,
![]() in such a manner that
it preserves the length of any ket upon which it acts
(i.e., if a ket is properly normalized at time
in such a manner that
it preserves the length of any ket upon which it acts
(i.e., if a ket is properly normalized at time ![]() then it will remain normalized at
all subsequent times
then it will remain normalized at
all subsequent times ![]() ).
This is always possible,
because the length of a ket possesses no physical significance. Thus,
we require that
).
This is always possible,
because the length of a ket possesses no physical significance. Thus,
we require that
![]() looks very much like the
spatial displacement
operator
looks very much like the
spatial displacement
operator ![]() introduced in Section 2.8. However, there are some
important differences between time evolution and spatial displacement. In general,
we do expect the expectation value of a given observable
introduced in Section 2.8. However, there are some
important differences between time evolution and spatial displacement. In general,
we do expect the expectation value of a given observable ![]() to
evolve with time, even if the system is left in a state of undisturbed motion
(after all, time evolution has no meaning unless something observable
changes with time). The triple product
to
evolve with time, even if the system is left in a state of undisturbed motion
(after all, time evolution has no meaning unless something observable
changes with time). The triple product
![]() can evolve
either because the ket
can evolve
either because the ket ![]() evolves and the operator
evolves and the operator ![]() stays constant,
the ket
stays constant,
the ket ![]() stays constant and the operator
stays constant and the operator ![]() evolves, or both
the ket
evolves, or both
the ket ![]() and the operator
and the operator ![]() evolve.
Because we are already committed to evolving state kets, according to Equation (3.3),
let us assume that the time evolution operator
evolve.
Because we are already committed to evolving state kets, according to Equation (3.3),
let us assume that the time evolution operator ![]() can be chosen in such a
manner that the operators representing the dynamical variables of the
system do not
evolve in time (unless they contain some specific time dependence).
can be chosen in such a
manner that the operators representing the dynamical variables of the
system do not
evolve in time (unless they contain some specific time dependence).
![]() then
then
![]() for any ket
for any ket ![]() . Thus, the
limit
. Thus, the
limit
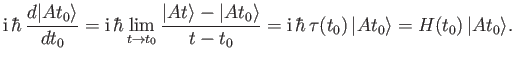
![]() that is, presumably, a characteristic
of the dynamical system under investigation.
that is, presumably, a characteristic
of the dynamical system under investigation.
![]() displaces the system along the
displaces the system along the ![]() -axis from
-axis from ![]() to
to ![]() then
then
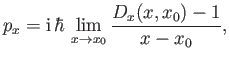
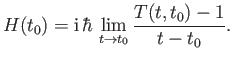
![]() into Equation (3.10) yields
into Equation (3.10) yields