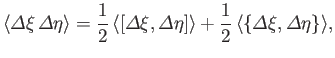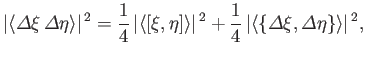Next: Continuous Spectra
Up: Fundamental Concepts
Previous: Compatible Observables
We have seen that if  and
and 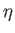 are two noncommuting observables then
a determination of the value of
are two noncommuting observables then
a determination of the value of  leaves the value of
leaves the value of 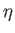 uncertain,
and vice versa. It is possible to quantify this uncertainty. For
a general observable
uncertain,
and vice versa. It is possible to quantify this uncertainty. For
a general observable  , we can define an Hermitian operator
, we can define an Hermitian operator
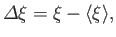 |
(1.71) |
where the expectation value is taken over the particular physical state under
consideration. It is obvious that the expectation value of
 is zero.
The expectation value of
is zero.
The expectation value of
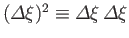 is termed
the variance of
is termed
the variance of  , and is, in general, non-zero. In fact,
it is easily demonstrated that
, and is, in general, non-zero. In fact,
it is easily demonstrated that
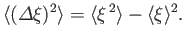 |
(1.72) |
The variance of  is a measure of the uncertainty in the value of
is a measure of the uncertainty in the value of  for
the particular state in question (i.e., it is a measure of the width of the
distribution of likely values of
for
the particular state in question (i.e., it is a measure of the width of the
distribution of likely values of  about the expectation value).
If the variance is zero then there is no uncertainty, and a measurement of
about the expectation value).
If the variance is zero then there is no uncertainty, and a measurement of  is bound to give the expectation value,
is bound to give the expectation value,
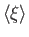 .
.
Consider the Schwarz inequality,
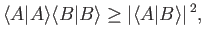 |
(1.73) |
which is analogous to
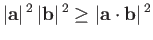 |
(1.74) |
in Euclidian space. This inequality can be proved by noting that
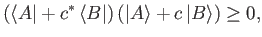 |
(1.75) |
where 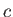 is any complex number. If
is any complex number. If 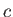 takes the special value
takes the special value
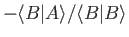 then the previous inequality reduces to
then the previous inequality reduces to
 |
(1.76) |
which is equivalent to the Schwarz inequality.
Let us substitute
into the Schwarz inequality, where the blank ket 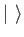 stands for any
general ket. We find
stands for any
general ket. We find
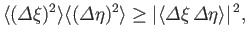 |
(1.79) |
where use has been made of the fact that
 and
and
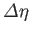 are
Hermitian operators. Note that
are
Hermitian operators. Note that
![$\displaystyle {\mit\Delta} \xi \,{\mit\Delta} \eta= \frac{1}{2} \left[ {\mit\De...
...} \eta\right] +\frac{1}{2} \left\{ {\mit\Delta} \xi, {\mit\Delta} \eta\right\},$](img192.png) |
(1.80) |
where the commutator,
![$ \left[ {\mit\Delta} \xi, {\mit\Delta} \eta\right]$](img193.png) ,
and the anti-commutator,
,
and the anti-commutator,
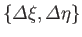 , are defined
, are defined
respectively.
The commutator is clearly anti-Hermitian,
![$\displaystyle (\left[ {\mit\Delta} \xi, {\mit\Delta} \eta\right])^{\dag } = ({\...
...a}\xi\, {\mit\Delta}\eta = - \left[ {\mit\Delta} \xi, {\mit\Delta} \eta\right],$](img199.png) |
(1.83) |
whereas the anti-commutator is obviously Hermitian. Now, it is easily
demonstrated that the expectation value of an Hermitian operator is a real
number, whereas the expectation value of an anti-Hermitian operator is
an imaginary number. (See Exercise 11.) It follows that the right-hand side of
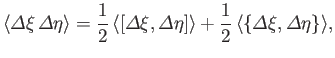 |
(1.84) |
consists of the sum of an imaginary and a real number.
Taking the modulus squared of both sides gives
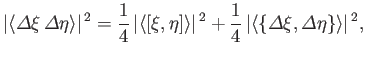 |
(1.85) |
where use has been made of
 , et cetera.
The final term on the right-hand side of the previous expression is positive definite, so we can write
, et cetera.
The final term on the right-hand side of the previous expression is positive definite, so we can write
![$\displaystyle \langle ({\mit\Delta} \xi)^{\,2}\rangle\, \langle ({\mit\Delta} \...
...{\,2}\geq \frac{1}{4} \, \vert\langle\left[ \xi, \eta\right]\rangle\vert^{\,2},$](img203.png) |
(1.86) |
where use has been made of Equation (1.79). The previous expression is termed the
uncertainty relation. According to this relation, an exact knowledge
of the value of  (i.e.,
(i.e.,
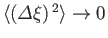 )
implies no knowledge whatsoever of the value of
)
implies no knowledge whatsoever of the value of 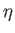 (i.e.,
(i.e.,
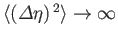 ),
and vice versa. The one exception to this rule is when
),
and vice versa. The one exception to this rule is when  and
and 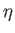 commute, in which case exact knowledge of
commute, in which case exact knowledge of  does not necessarily imply
no knowledge of
does not necessarily imply
no knowledge of 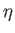 .
.



Next: Continuous Spectra
Up: Fundamental Concepts
Previous: Compatible Observables
Richard Fitzpatrick
2016-01-22
![$\displaystyle {\mit\Delta} \xi \,{\mit\Delta} \eta= \frac{1}{2} \left[ {\mit\De...
...} \eta\right] +\frac{1}{2} \left\{ {\mit\Delta} \xi, {\mit\Delta} \eta\right\},$](img192.png)