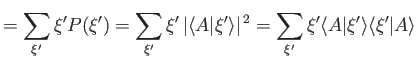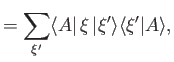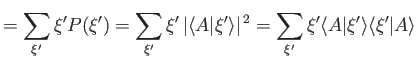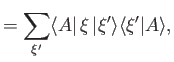Next: Degeneracy
Up: Fundamental Concepts
Previous: Measurements
Expectation Values
Consider an ensemble of microscopic systems prepared in the
same (normalized) initial state 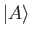 . Suppose that a measurement of the observable
. Suppose that a measurement of the observable  is
made on each system. We know that each measurement yields the value
is
made on each system. We know that each measurement yields the value 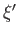 with
probability
with
probability 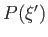 . What is the mean value of the measurement? This quantity,
which is generally referred to as the expectation value of
. What is the mean value of the measurement? This quantity,
which is generally referred to as the expectation value of  , is
given by
, is
given by
which reduces to
 |
(1.62) |
with the aid of Equation (1.57).
Consider the identity operator, 1. All states are eigenstates of this operator
with the eigenvalue unity. Thus, the expectation value of this operator
is always unity: that is,
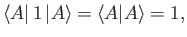 |
(1.63) |
for all 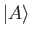 . Note that it is only possible to normalize a given
state ket
. Note that it is only possible to normalize a given
state ket 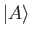 , such that Equation (1.63) is satisfied, because of the more general
property (1.22) of the norm. This property depends on the previously adopted correspondence,
(1.11) and (1.16), between the elements of a ket space and those of its
dual bra space.
, such that Equation (1.63) is satisfied, because of the more general
property (1.22) of the norm. This property depends on the previously adopted correspondence,
(1.11) and (1.16), between the elements of a ket space and those of its
dual bra space.



Next: Degeneracy
Up: Fundamental Concepts
Previous: Measurements
Richard Fitzpatrick
2016-01-22