Next: Counter-Propagating Beam Instability Up: Waves in Warm Plasmas Previous: Electrostatic Waves Contents
Consider the dispersion relation (7.23) for an electrostatic plasma wave in an unmagnetized quasi-neutral plasma with stationary ions. This relation can be written
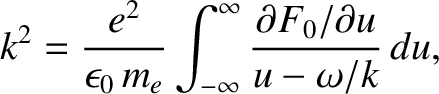 |
(7.125) |
 |
(7.127) |
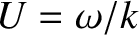 .
Taking
.
Taking 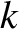 to be real and positive, the question of whether the system is stable or not is equivalent to asking
whether Equation (7.126) is satisfied for any value of
to be real and positive, the question of whether the system is stable or not is equivalent to asking
whether Equation (7.126) is satisfied for any value of 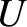 lying in the upper half of the complex plane.
lying in the upper half of the complex plane.
To answer the previous question, we employ a standard result in complex variable theory which states that
the number of zeros minus the number of poles of
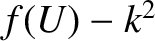 in a given region of the complex
in a given region of the complex 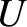 plane
is
plane
is
 times the increase in the argument of
times the increase in the argument of
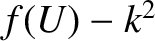 as
as 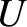 moves once counter-clockwise
around the boundary of this region (Flanigan 2010). To determine the latter quantity, we construct
what is known as a Nyquist diagram (Nyquist 1932). Because the region in which we are interested is the
upper-half complex plane, we let
moves once counter-clockwise
around the boundary of this region (Flanigan 2010). To determine the latter quantity, we construct
what is known as a Nyquist diagram (Nyquist 1932). Because the region in which we are interested is the
upper-half complex plane, we let 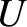 follow the semi-circular path shown in Figure 7.10(a), and
plot the corresponding path followed in the complex plane by
follow the semi-circular path shown in Figure 7.10(a), and
plot the corresponding path followed in the complex plane by 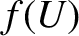 , as illustrated in Figure 7.10(b).
Now,
, as illustrated in Figure 7.10(b).
Now,
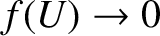 as
as
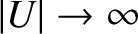 . Hence, if the radius of the semicircle in Figure 7.10(a)
tends to infinity then only that part of the contour running along the real axis is important, and the
. Hence, if the radius of the semicircle in Figure 7.10(a)
tends to infinity then only that part of the contour running along the real axis is important, and the 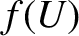 contour
starts and finishes at the origin. Because the function
contour
starts and finishes at the origin. Because the function 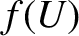 is analytic in the upper-half
is analytic in the upper-half  plane, by virtue of the way
in which it is defined, the number of zeros of
plane, by virtue of the way
in which it is defined, the number of zeros of
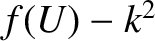 is equal to the change in argument (divided by
is equal to the change in argument (divided by 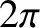 ) of this
quantity as the path shown in Figure 7.10(b) is followed. However, this is just the number of times that the path
encircles the point
) of this
quantity as the path shown in Figure 7.10(b) is followed. However, this is just the number of times that the path
encircles the point  . Hence, the criterion for instability is that the path should encircle part of the positive real axis.
Thus, in Figure 7.10(b), the system is unstable for the indicated values of
. Hence, the criterion for instability is that the path should encircle part of the positive real axis.
Thus, in Figure 7.10(b), the system is unstable for the indicated values of  (Cairns 1985).
(Cairns 1985).
In an unstable system, there must exist a point such as 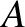 in Figure 7.10(b) where the
in Figure 7.10(b) where the 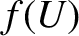 contour
crosses the real axis going from negative to positive imaginary part. Now, as
contour
crosses the real axis going from negative to positive imaginary part. Now, as
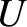 moves along the real axis [cf., Equation (7.26)],
moves along the real axis [cf., Equation (7.26)],
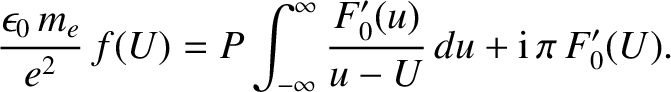 |
(7.128) |
 , corresponding to
, corresponding to 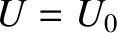 (say), it must be the case that
(say), it must be the case that
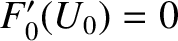 . Furthermore,
. Furthermore,
 must go from being negative to being positive as
must go from being negative to being positive as 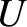 passes through
passes through 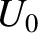 from below.
This implies that
from below.
This implies that 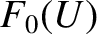 attains a minimum at
attains a minimum at 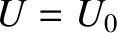 . In other words, a necessary condition for the distribution function
. In other words, a necessary condition for the distribution function 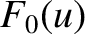 to be unstable
is that it should attain
a minimum value at some finite value of
to be unstable
is that it should attain
a minimum value at some finite value of 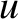 .
A further condition to be satisfied is that the
real part of
.
A further condition to be satisfied is that the
real part of 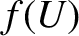 be positive at
be positive at 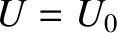 . In other words,
. In other words,
 |
(7.129) |
 has been chosen as the constant of integration in order to again make it unnecessary to take the principal part.
The previous relation is called the Penrose condition, and is a necessary and sufficient condition for
instability, assuming that
has been chosen as the constant of integration in order to again make it unnecessary to take the principal part.
The previous relation is called the Penrose condition, and is a necessary and sufficient condition for
instability, assuming that 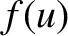 attains a minimum value at
attains a minimum value at 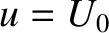 (Penrose 1960).
(Penrose 1960).
The previous discussion implies that a single-humped velocity distribution function, such as a Maxwellian, is absolutely stable to
velocity-space instabilities (Gardner 1963). This follows because there is no finite value of 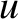 at which such a distribution function
attains a minimum value. In fact, assuming that the distribution function,
at which such a distribution function
attains a minimum value. In fact, assuming that the distribution function, 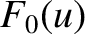 , is such that
, is such that
 as
as
 , we deduce that an unstable distribution function must possess at least
one minimum and two maxima for
, we deduce that an unstable distribution function must possess at least
one minimum and two maxima for 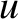 in the range
in the range
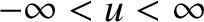 .
.