Next: Waves in Warm Plasmas Up: Waves in Inhomogeneous Plasmas Previous: Ionospheric Radio Wave Propagation Contents
 , in a linear dielectric medium is related to the electric field-strength,
, in a linear dielectric medium is related to the electric field-strength,  ,
according to
,
according to
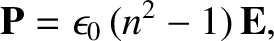
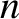 is the refractive index. Any divergence of the polarization field is associated with a bound charge density
is the refractive index. Any divergence of the polarization field is associated with a bound charge density
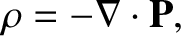
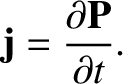
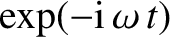 time variation of the wave fields, demonstrate from Maxwell's equations that
time variation of the wave fields, demonstrate from Maxwell's equations that
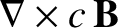 |
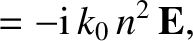 |
|
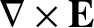 |
 |
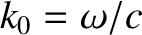 .
.
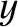 -direction, that propagates in the
-direction, that propagates in the 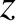 -direction through
a medium of refractive index
-direction through
a medium of refractive index 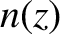 . Assuming that
. Assuming that
 |
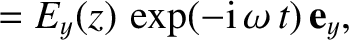 |
|
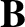 |
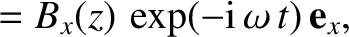 |
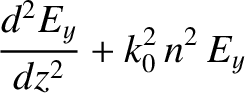 |
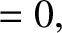 |
|
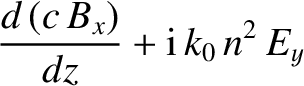 |
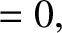 |
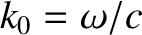 .
.
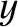 -direction, that propagates in the
-direction, that propagates in the 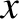 -
-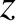 plane
through a medium of refractive index
plane
through a medium of refractive index 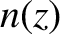 . Assuming that
. Assuming that
 |
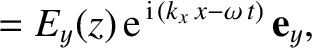 |
|
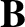 |
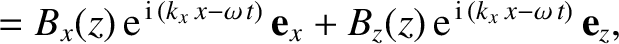 |
 |
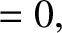 |
|
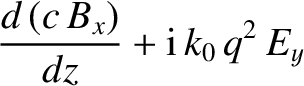 |
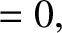 |
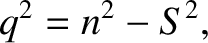
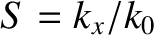 , and
, and
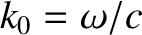 .
.
Show that the WKB solutions take the form
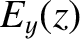 |
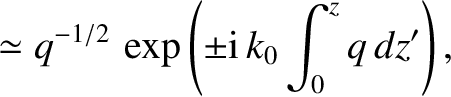 |
|
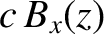 |
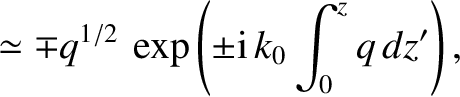 |

 -
- -plane, that propagates in the
-plane, that propagates in the  -
-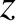 plane
through a medium of refractive index
plane
through a medium of refractive index 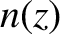 . Assuming that
. Assuming that
 |
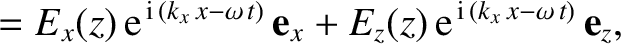 |
|
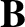 |
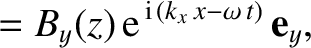 |
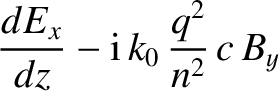 |
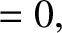 |
|
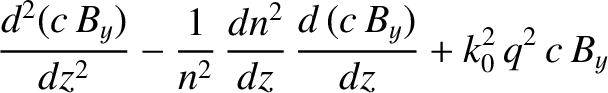 |
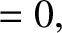 |
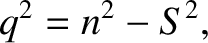
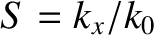 , and
, and
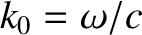 .
.
Show that the WKB solutions take the form
 |
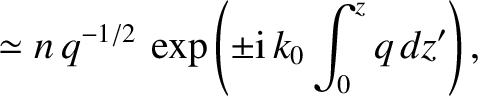 |
|
 |
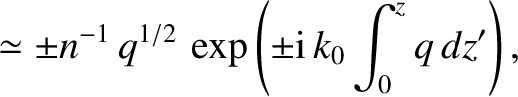 |
![$\displaystyle \frac{1}{k_0^{2}}\left\vert\frac{3}{4}\left(\frac{1}{q^2}\,\frac{...
...2n}{dz^2}-2\,\left(\frac{1}{n}\,\frac{dn}{dz}\right)^2\right]\right\vert\ll 1.
$](img2199.png)
 is launched vertically from ground level, travels upward into the ionosphere,
is reflected, and returns to ground level. If
is launched vertically from ground level, travels upward into the ionosphere,
is reflected, and returns to ground level. If
 is the net travel time of the pulse then the so-called
equivalent height of reflection is defined
is the net travel time of the pulse then the so-called
equivalent height of reflection is defined
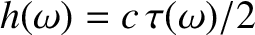 . It follows that
. It follows that 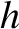 is the altitude of the reflection
layer calculated on the assumption that the pulse always travels at the velocity of light in vacuum. Let
is the altitude of the reflection
layer calculated on the assumption that the pulse always travels at the velocity of light in vacuum. Let
 be the
ionospheric plasma frequency, where
be the
ionospheric plasma frequency, where  measures altitude above the ground. Neglect collisions and the Earth's magnetic field.
measures altitude above the ground. Neglect collisions and the Earth's magnetic field.
![$\displaystyle h(\omega) = \int_0^{z_0(\omega)}\frac{\omega}{\left[\omega^2- {\mit\Pi}_e^{2}(z)\right]^{1/2}}\,dz,
$](img2203.png)
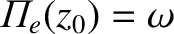 .
.
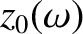 is a monotonically increasing function of
is a monotonically increasing function of 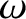 then the previous integral can be inverted to
give
then the previous integral can be inverted to
give
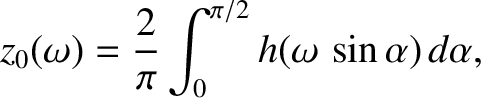
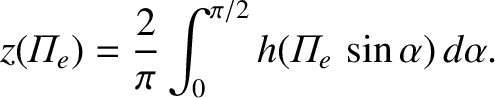
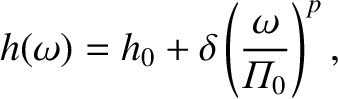
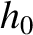 ,
, 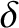 , and
, and
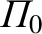 are positive constants, then
are positive constants, then
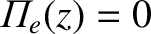 for
for  , and
, and
![$\displaystyle {\mit\Pi}_e(z) =\left[\frac{\pi\,{\Gamma}(1+p)}{{\Gamma}(1/2+p/2)...
.../2)}\right]^{1/p} \frac{{\mit\Pi}_0}{2}\left(\frac{z-h_0}{\delta}\right)^{1/p}
$](img2213.png)
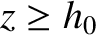 . Here,
. Here,
 is a gamma function (Abramowitz and Stegun 1965).
is a gamma function (Abramowitz and Stegun 1965).
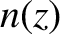 , of the ionosphere is given by
, of the ionosphere is given by
 for
for 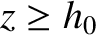 ,
and
,
and 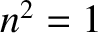 for
for  , where
, where  and
and 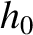 are positive constants, and the Earth's magnetic field and curvature are both neglected.
Here,
are positive constants, and the Earth's magnetic field and curvature are both neglected.
Here,  measures altitude above the Earth's surface.
measures altitude above the Earth's surface.
 to the vertical. Show that the packet returns to Earth a
distance
to the vertical. Show that the packet returns to Earth a
distance
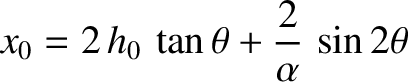
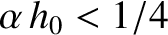 then for some values of
then for some values of  the previous equation is satisfied
by three different values of
the previous equation is satisfied
by three different values of  . In other words, wave packets can travel from the transmitter to the receiver via one of
three different paths. Show that the critical case
. In other words, wave packets can travel from the transmitter to the receiver via one of
three different paths. Show that the critical case
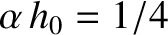 corresponds to
corresponds to
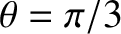 and
and
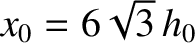 .
.
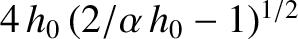 from the transmitter, provided that
from the transmitter, provided that
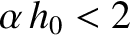 .
.