Next: Wave Polarization Up: Waves in Cold Plasmas Previous: Cold-Plasma Dielectric Permittivity Contents
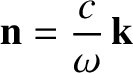 |
(5.40) |
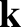 ,
and whose magnitude,
,
and whose magnitude,
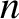 , is the refractive index (i.e., the ratio of the
velocity of light in vacuum to the phase-velocity).
Equation (5.9) can be rewritten
, is the refractive index (i.e., the ratio of the
velocity of light in vacuum to the phase-velocity).
Equation (5.9) can be rewritten
Without loss of generality, we can assume that the equilibrium
magnetic field is directed along the 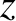 -axis, and that the wavevector,
-axis, and that the wavevector,
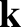 , lies in the
, lies in the 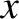 -
-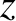 plane. Let
plane. Let 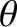 be the angle subtended between
be the angle subtended between
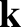 and
and 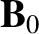 . The eigenmode equation (5.41) can be written
. The eigenmode equation (5.41) can be written
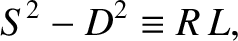 |
(5.43) |
The dispersion relation (5.44) is evidently a quadratic in 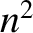 , with
two roots.
The solution can be written
, with
two roots.
The solution can be written
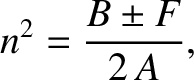 |
(5.48) |
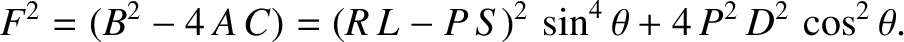 |
(5.49) |
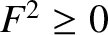 . It follows that
. It follows that 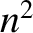 is always real, which implies
that
is always real, which implies
that 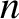 is either purely real, or purely imaginary. In other words, the
cold-plasma dispersion relation describes waves that either propagate
without evanescense, or decay without spatial oscillation.
The two roots
of opposite sign for
is either purely real, or purely imaginary. In other words, the
cold-plasma dispersion relation describes waves that either propagate
without evanescense, or decay without spatial oscillation.
The two roots
of opposite sign for 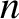 , corresponding to a particular root for
, corresponding to a particular root for 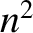 , simply describe
waves of the same type propagating, or decaying, in opposite directions.
, simply describe
waves of the same type propagating, or decaying, in opposite directions.
The dispersion relation (5.44) can also be written
For the special case of wave propagation parallel to the magnetic field (i.e.,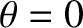 ), the previous expression reduces to
Likewise, for the special case of propagation perpendicular to the
field (i.e.,
), the previous expression reduces to
Likewise, for the special case of propagation perpendicular to the
field (i.e.,
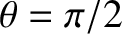 ), Equation (5.50) yields
), Equation (5.50) yields
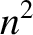 |
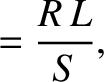 |
(5.54) |
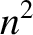 |
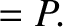 |
(5.55) |