Next: Fluid Equations Up: Plasma Fluid Theory Previous: Moments of Collision Operator Contents
 |
(4.33) |
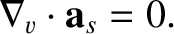 |
(4.34) |
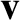 is independent of
is independent of 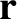 .
.
The 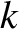 th moment of the kinetic equation is obtained
by multiplying the previous equation by
th moment of the kinetic equation is obtained
by multiplying the previous equation by 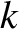 powers of
powers of 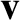 , and integrating
over velocity space. The flow term is simplified by pulling the
divergence outside the velocity integral. The acceleration term is treated by partial
integration. These two terms couple the
, and integrating
over velocity space. The flow term is simplified by pulling the
divergence outside the velocity integral. The acceleration term is treated by partial
integration. These two terms couple the 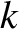 th moment
to the
th moment
to the 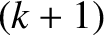 th and
th and 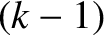 th moments, respectively.
th moments, respectively.
Making use of the collisional conservation laws, the zeroth moment of Equation (4.35)
yields the continuity equation for species  :
:
 :
Finally, the contracted second moment yields the energy conservation
equation for species
:
Finally, the contracted second moment yields the energy conservation
equation for species  :
:
The interpretation of Equations (4.36)–(4.38) as conservation laws is
straightforward. Suppose that 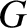 is some physical quantity (for instance, the
total number of particles, the total energy, and so on), and
is some physical quantity (for instance, the
total number of particles, the total energy, and so on), and
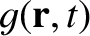 is its density:
is its density:
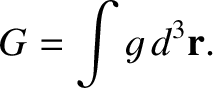 |
(4.39) |
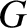 is conserved then
is conserved then 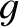 must evolve according to
must evolve according to
 |
(4.40) |
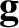 is the flux density of
is the flux density of 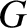 , and
, and
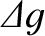 is the
local rate per unit volume at which
is the
local rate per unit volume at which 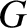 is created, or exchanged with other
entities in the fluid. According to the previous equation, the density of
is created, or exchanged with other
entities in the fluid. According to the previous equation, the density of 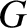 at some point
changes because there is net flow of
at some point
changes because there is net flow of 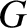 towards or away from that
point (characterized by the divergence term), or because of local
sources or sinks of
towards or away from that
point (characterized by the divergence term), or because of local
sources or sinks of 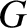 (characterized by the right-hand side).
(characterized by the right-hand side).
Applying this reasoning to Equation (4.36), we see that
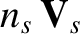 is indeed the
species-
is indeed the
species- particle flux density, and that there are no local sources or sinks of
species-
particle flux density, and that there are no local sources or sinks of
species- particles.4.1 From Equation (4.37), it is apparent that the stress tensor,
particles.4.1 From Equation (4.37), it is apparent that the stress tensor, 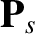 , is the species-
, is the species- momentum flux density, and that
the species-
momentum flux density, and that
the species- momentum is changed locally by the Lorentz force, and by collisional
friction with other species. Finally, from Equation (4.38), we see that
momentum is changed locally by the Lorentz force, and by collisional
friction with other species. Finally, from Equation (4.38), we see that
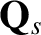 is indeed the species-
is indeed the species- energy flux density, and that the
species-
energy flux density, and that the
species- energy is changed locally by electrical work, energy exchange with
other species, and frictional heating.
energy is changed locally by electrical work, energy exchange with
other species, and frictional heating.