Next: Collisional Conservation Laws Up: Collisions Previous: Two-Body Elastic Collisions Contents
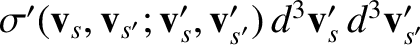 be the number of species-
be the number of species- particles
per unit time, per unit flux of species-
particles
per unit time, per unit flux of species- particles incident with velocity
particles incident with velocity 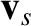 on a species-
on a species- particle of velocity
particle of velocity
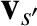 ,
that are scattered such that
the species-
,
that are scattered such that
the species- particles emerge in the velocity range
particles emerge in the velocity range
 to
to
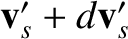 and the species-
and the species- particle emerges in the velocity range
particle emerges in the velocity range
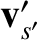 to
to
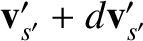 (Reif 1965).
Assuming that the scattering process is reversible in time and space (which is certainly the
case for two-body Coulomb collisions), the
corresponding quantity for the inverse process must be equal to that for the forward process (Reif 1965). In other words,
However, it is easily demonstrated from Equations (3.12) and (3.13) that
The result
(Reif 1965).
Assuming that the scattering process is reversible in time and space (which is certainly the
case for two-body Coulomb collisions), the
corresponding quantity for the inverse process must be equal to that for the forward process (Reif 1965). In other words,
However, it is easily demonstrated from Equations (3.12) and (3.13) that
The result
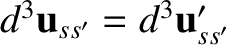 follows from the fact that the vectors
follows from the fact that the vectors
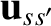 and
and
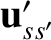 differ only
in direction. Hence, we deduce that
differ only
in direction. Hence, we deduce that
The rate of decrease in the number of species- particles located between
particles located between 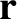 and
and
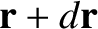 ,
and having velocities in the range
,
and having velocities in the range 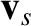 to
to
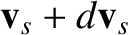 , due to scattering of species-
, due to scattering of species- particles by species-
particles by species- particles is
obtained by multiplying
particles is
obtained by multiplying
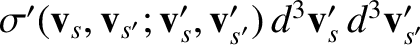 by the the relative flux,
by the the relative flux,
 ,
of species-
,
of species- particles incident on a species-
particles incident on a species- particle, then multiplying by the number of species-
particle, then multiplying by the number of species- particles,
particles,
 , that can do the scattering, and, finally, summing over all possible
species-
, that can do the scattering, and, finally, summing over all possible
species- initial velocities, and all possible species-
initial velocities, and all possible species- and species-
and species- final velocities.
In other words,
final velocities.
In other words,
 . Moreover,
. Moreover,
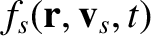 and
and
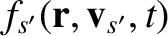 are the ensemble-averaged distribution
functions for species-
are the ensemble-averaged distribution
functions for species- and species-
and species- particles, respectively.
particles, respectively.
In writing the previous expression, we have assumed that the distribution functions 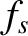 and
and 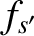 are uncorrelated. This assumption is reasonable provided that the mean-free-path is much longer than the effective range of
the inter-particle force. (This follows because, before they encounter one another, two colliding particles originate at different points that are typically separated by
a mean-free-path. However, the typical correlation length is of similar magnitude to the range of the inter-particle force.)
In writing the previous expression, we have also implicitly assumed that the inter-particle force responsible for the collisions is sufficiently short-range that
the particle position vectors do not change appreciably (on a macroscopic lengthscale) during a collision. (Both of the previous
assumptions are valid in a conventional weakly coupled plasma because the range of the inter-particle force is of order the Debye
length, which is assumed to be much smaller than any macroscopic lengthscale. Moreover, the mean-free-path is much
longer than the Debye length—see Section 1.7.)
are uncorrelated. This assumption is reasonable provided that the mean-free-path is much longer than the effective range of
the inter-particle force. (This follows because, before they encounter one another, two colliding particles originate at different points that are typically separated by
a mean-free-path. However, the typical correlation length is of similar magnitude to the range of the inter-particle force.)
In writing the previous expression, we have also implicitly assumed that the inter-particle force responsible for the collisions is sufficiently short-range that
the particle position vectors do not change appreciably (on a macroscopic lengthscale) during a collision. (Both of the previous
assumptions are valid in a conventional weakly coupled plasma because the range of the inter-particle force is of order the Debye
length, which is assumed to be much smaller than any macroscopic lengthscale. Moreover, the mean-free-path is much
longer than the Debye length—see Section 1.7.)
By analogy with Equation (3.19), the rate of increase in the number of species- particles located between
particles located between 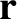 and
and
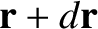 ,
and having velocities in the range
,
and having velocities in the range 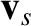 to
to
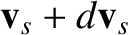 , due to the recoil of species-
, due to the recoil of species- particles that scatter species-
particles that scatter species- particles is
particles is
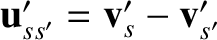 . Making use of Equations (3.16) and (3.17), as well as
. Making use of Equations (3.16) and (3.17), as well as
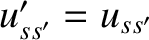 , we obtain
, we obtain
The net rate of change of the distribution function of species- particles with velocities
particles with velocities 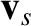 (at position
(at position 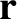 and time
and time 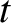 ) due to collisions with
species-
) due to collisions with
species- particles [i.e., the collision operator—see Equation (3.9)] is given by
particles [i.e., the collision operator—see Equation (3.9)] is given by
![$\displaystyle C_{ss'}(f_s,f_{s'}) =\left[\frac{\partial f_s({\bf r},{\bf v}_s,t...
...ss'} + \left[\frac{\partial f_s({\bf r},{\bf v}_s,t)}{\partial t}\right]_{s's}.$](img631.png) |
(3.22) |
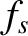 ,
, 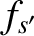 ,
, 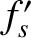 , and
, and  are short-hand for
are short-hand for
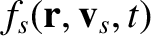 ,
,
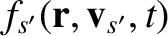 ,
,
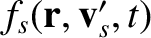 , and
, and
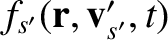 , respectively.
The previous expression is known as the Boltzmann collision operator (Boltzmann 1995).
By an analogous argument, the net rate of change of the distribution function of species-
, respectively.
The previous expression is known as the Boltzmann collision operator (Boltzmann 1995).
By an analogous argument, the net rate of change of the distribution function of species- particles with velocities
particles with velocities
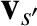 (at position
(at position 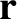 and time
and time 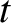 ) due to collisions with species-
) due to collisions with species- particles is given by
particles is given by
Expression (3.23) for the Boltzmann collision operator can be further simplified for
elastic collisions because, in this case, the collision cross-section
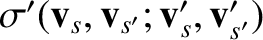 is a function only of the magnitude of the relative velocity vector,
is a function only of the magnitude of the relative velocity vector,
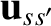 , and its change in direction as a result of the collision. Furthermore, the integral over the final velocities
, and its change in direction as a result of the collision. Furthermore, the integral over the final velocities
 and
and
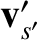 reduces
to an integral over all solid angles for the change in direction of
reduces
to an integral over all solid angles for the change in direction of
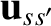 . Thus,
we can write
. Thus,
we can write
 . Here,
. Here, 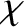 is the angle through which the direction of
is the angle through which the direction of
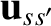 is deflected as a consequence of the
collision (see Figure 3.1), and
is deflected as a consequence of the
collision (see Figure 3.1), and 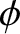 is an azimuthal angle that determines the orientation of the plane in
which the vector
is an azimuthal angle that determines the orientation of the plane in
which the vector
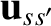 is confined during the collision. (See Section 3.6.) Moreover,
is confined during the collision. (See Section 3.6.) Moreover,
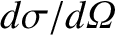 is a conventional
differential scattering cross-section (Reif 1965). Hence, we obtain
Note, finally, that if we exchange the identities of species-
is a conventional
differential scattering cross-section (Reif 1965). Hence, we obtain
Note, finally, that if we exchange the identities of species- and species-
and species- particles in Equation (3.25) then
particles in Equation (3.25) then
 , but
, but
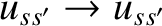 ,
,
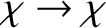 , and
, and
 . Thus, we conclude that
. Thus, we conclude that