Next: Third Adiabatic Invariant Up: Charged Particle Motion Previous: Equatorial Ring Current Contents
Recall that an adiabatic invariant is the lowest order approximation to a Poincaré invariant:
 |
(2.115) |
 correspond to the trajectory of
a guiding center as a charged
particle trapped in the
Earth's magnetic field
executes a bounce orbit. Of course, this trajectory does not quite close,
because of the slow azimuthal drift of particles around the Earth. However,
it is easily demonstrated that
the azimuthal displacement of the end point of the trajectory, with respect to
the beginning point, is similar in magnitude to the gyroradius. Thus, in the limit
in which the ratio of the gyroradius,
correspond to the trajectory of
a guiding center as a charged
particle trapped in the
Earth's magnetic field
executes a bounce orbit. Of course, this trajectory does not quite close,
because of the slow azimuthal drift of particles around the Earth. However,
it is easily demonstrated that
the azimuthal displacement of the end point of the trajectory, with respect to
the beginning point, is similar in magnitude to the gyroradius. Thus, in the limit
in which the ratio of the gyroradius, 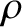 , to the variation lengthscale of the
magnetic field,
, to the variation lengthscale of the
magnetic field, 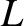 , tends to zero, the trajectory of the guiding center
can be regarded as being approximately closed,
and the actual particle trajectory conforms very closely
to that of the guiding center. Thus, the adiabatic invariant associated with
the bounce motion can be written
, tends to zero, the trajectory of the guiding center
can be regarded as being approximately closed,
and the actual particle trajectory conforms very closely
to that of the guiding center. Thus, the adiabatic invariant associated with
the bounce motion can be written
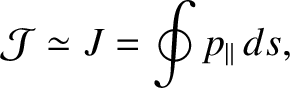 |
(2.116) |
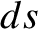 is an element of arc-length along the
field-line, and
is an element of arc-length along the
field-line, and
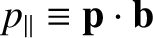 .
Using
.
Using
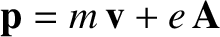 , the previous
expression yields
, the previous
expression yields
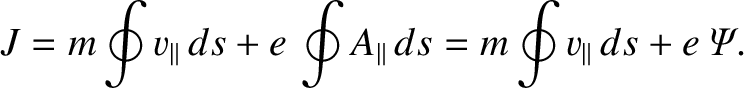 |
(2.117) |
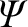 is the total magnetic flux enclosed by the curve—which,
in this case, is obviously zero. Thus, the so-called second adiabatic invariant, or
longitudinal adiabatic invariant, takes the form
is the total magnetic flux enclosed by the curve—which,
in this case, is obviously zero. Thus, the so-called second adiabatic invariant, or
longitudinal adiabatic invariant, takes the form
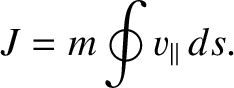 |
(2.118) |
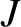 is not particularly rigorous. In fact, the rigorous proof
that
is not particularly rigorous. In fact, the rigorous proof
that 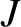 is an adiabatic invariant was first given by Northrop and Teller (Northrop and Teller 1960). Of course,
is an adiabatic invariant was first given by Northrop and Teller (Northrop and Teller 1960). Of course, 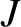 is only a constant of the motion
for particles trapped in the inner magnetosphere provided the
magnetospheric
magnetic field varies on timescales that are much longer than the bounce time,
is only a constant of the motion
for particles trapped in the inner magnetosphere provided the
magnetospheric
magnetic field varies on timescales that are much longer than the bounce time,
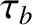 . Because the bounce time for MeV energy protons and electrons is,
at most, a few seconds, this is not a particularly onerous constraint.
. Because the bounce time for MeV energy protons and electrons is,
at most, a few seconds, this is not a particularly onerous constraint.
![\includegraphics[height=1.8in]{Chapter02/fig2_4.eps}](img496.png) |
The invariance of 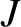 is of great importance for charged particle
dynamics in the Earth's inner magnetosphere. It turns out that the
Earth's magnetic field is distorted from pure axisymmetry by the action of
the solar wind, as illustrated in Figure 2.4. Because of this asymmetry, there
is no particular reason to believe that a particle will return to its
earlier trajectory as it makes a full circuit around the Earth. In other words,
the particle may well end up on a different field-line when it returns to
the same azimuthal angle. However, at a given azimuthal angle, each
field-line has a different length between mirror points, and a different
variation of the field-strength,
is of great importance for charged particle
dynamics in the Earth's inner magnetosphere. It turns out that the
Earth's magnetic field is distorted from pure axisymmetry by the action of
the solar wind, as illustrated in Figure 2.4. Because of this asymmetry, there
is no particular reason to believe that a particle will return to its
earlier trajectory as it makes a full circuit around the Earth. In other words,
the particle may well end up on a different field-line when it returns to
the same azimuthal angle. However, at a given azimuthal angle, each
field-line has a different length between mirror points, and a different
variation of the field-strength, 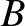 , between the mirror points (for a particle
with given energy,
, between the mirror points (for a particle
with given energy,  , and magnetic moment,
, and magnetic moment,  ). Thus, each field-line
represents a different value of
). Thus, each field-line
represents a different value of 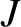 for that particle. So, if
for that particle. So, if 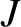 is
conserved, as well as
is
conserved, as well as  and
and  , then the particle
must return to the same field-line after precessing around the Earth.
In other words, the conservation of
, then the particle
must return to the same field-line after precessing around the Earth.
In other words, the conservation of 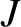 prevents charged particles from
spiraling radially in or out of the Van Allen belts as they rotate around the Earth.
This helps to explain the persistence of these belts.
prevents charged particles from
spiraling radially in or out of the Van Allen belts as they rotate around the Earth.
This helps to explain the persistence of these belts.