Next: Exercises Up: Waves in Inhomogeneous Plasmas Previous: Ray Tracing Contents
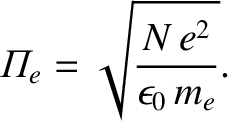 |
(6.110) |
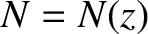 is the density of free electrons in the ionosphere, and
is the density of free electrons in the ionosphere, and
 is a coordinate that measures height above the surface of the Earth.
(The curvature of the Earth, the Earth's magnetic field, and collisions, are neglected in the following analysis.)
is a coordinate that measures height above the surface of the Earth.
(The curvature of the Earth, the Earth's magnetic field, and collisions, are neglected in the following analysis.)
Now,
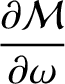 |
 |
(6.111) |
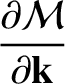 |
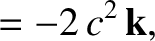 |
(6.112) |
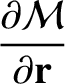 |
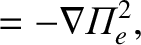 |
(6.113) |
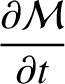 |
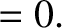 |
(6.114) |
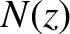 does not vary in time.
Furthermore, it follows from Equations (6.115)–(6.117), and the fact that
does not vary in time.
Furthermore, it follows from Equations (6.115)–(6.117), and the fact that
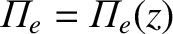 , that
a radio pulse that starts off at ground level propagating in the
, that
a radio pulse that starts off at ground level propagating in the  -
- plane, say,
will continue to propagate in this plane.
plane, say,
will continue to propagate in this plane.
For pulse propagation in the  -
- plane, we have
plane, we have
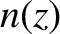 is the refractive index.
is the refractive index.
Let us assume that 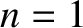 at
at 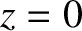 , which is equivalent to the
reasonable assumption that the atmosphere is non-ionized at ground level.
It follows from Equation (6.120) that
, which is equivalent to the
reasonable assumption that the atmosphere is non-ionized at ground level.
It follows from Equation (6.120) that
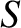 is the sine of the angle of incidence of the pulse, with respect to
the vertical axis, at ground level. Equations (6.121) and (6.122) yield
According to Equation (6.119), the plus sign corresponds to the upward trajectory
of the pulse, whereas the minus sign corresponds to the downward trajectory.
Finally, Equations (6.118), (6.119), (6.122), and (6.123)
yield the equations of motion of the pulse:
is the sine of the angle of incidence of the pulse, with respect to
the vertical axis, at ground level. Equations (6.121) and (6.122) yield
According to Equation (6.119), the plus sign corresponds to the upward trajectory
of the pulse, whereas the minus sign corresponds to the downward trajectory.
Finally, Equations (6.118), (6.119), (6.122), and (6.123)
yield the equations of motion of the pulse:
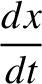 |
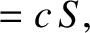 |
(6.124) |
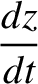 |
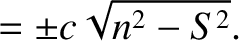 |
(6.125) |
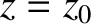 , when
The total distance traveled by the pulse (i.e., the distance
from its launch
point to the point where it intersects the Earth's surface again) is
, when
The total distance traveled by the pulse (i.e., the distance
from its launch
point to the point where it intersects the Earth's surface again) is
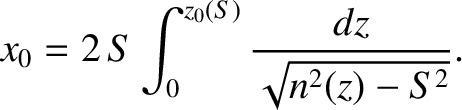 |
(6.127) |
In the limit in which the radio pulse is launched vertically (i.e.,
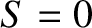 ) into the ionosphere, the turning point condition (6.126) reduces to
that characteristic of a cutoff (i.e.,
) into the ionosphere, the turning point condition (6.126) reduces to
that characteristic of a cutoff (i.e., 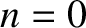 ). The WKB turning point
described in Equation (6.126) is a generalization of the conventional turning point,
which occurs when
). The WKB turning point
described in Equation (6.126) is a generalization of the conventional turning point,
which occurs when 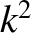 changes sign. Here,
changes sign. Here, 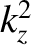 changes sign, while
changes sign, while
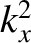 and
and 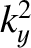 are constrained by symmetry (i.e.,
are constrained by symmetry (i.e.,  is constant,
and
is constant,
and 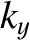 is zero).
is zero).
According to Equations (6.115)–(6.117) and (6.121), the equation of motion of the pulse can also be written
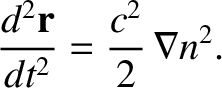 |
(6.128) |
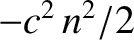 . Thus, if
. Thus, if
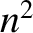 decreases linearly with increasing height above the
ground [which is the case if
decreases linearly with increasing height above the
ground [which is the case if  increases linearly with
increases linearly with  ] then the
trajectory of the pulse is a parabola.
] then the
trajectory of the pulse is a parabola.