Langmuir Sheaths
Virtually all terrestrial plasmas are contained within solid vacuum vessels. But, what happens to plasma in the immediate vicinity of a vessel wall? Actually, to a first approximation, when ions and electrons hit a solid surface they recombine and are lost to the plasma. Hence, we can
treat the wall as a perfect sink of particles. Now, given that the electrons in a plasma generally
move much faster than the ions, the initial electron flux into the wall greatly
exceeds the ion flux, assuming that the wall starts off
unbiased with respect to the plasma. Of course, this flux imbalance causes the wall to charge up negatively, and so
generates a potential barrier that repels the electrons, and thereby
reduces the electron flux.
Debye shielding
confines this barrier to a thin layer of plasma, whose thickness is a few
Debye lengths, coating the inside surface of the wall. This layer
is known as a plasma sheath or a Langmuir sheath.
The height of the potential barrier continues to grow as long
as there is a net flux of negative charge into the wall.
This process presumably comes to an end, and a steady-state is attained, when the potential barrier becomes sufficiently large to make electron flux equal to the ion flux (Hazeltine and Waelbroeck 2004).
Let us construct a one-dimensional model of an unmagnetized, steady-state, Langmuir sheath.
Suppose that the wall lies at 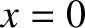 , and that the plasma occupies the
region
, and that the plasma occupies the
region  . Let us treat the ions and the electrons inside the sheath
as collisionless fluids.
The ion and electron equations of
motion are thus written
. Let us treat the ions and the electrons inside the sheath
as collisionless fluids.
The ion and electron equations of
motion are thus written
respectively. Here,
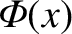 is the electrostatic potential. Moreover, we have
assumed uniform ion and electron temperatures,
is the electrostatic potential. Moreover, we have
assumed uniform ion and electron temperatures, 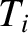 and
and  ,
respectively, for the sake of simplicity. We have also neglected any off-diagonal
terms in the ion and electron stress-tensors, because these terms are
comparatively small.
Note that quasi-neutrality
does not apply inside the sheath, and so the ion and
electron number densities,
,
respectively, for the sake of simplicity. We have also neglected any off-diagonal
terms in the ion and electron stress-tensors, because these terms are
comparatively small.
Note that quasi-neutrality
does not apply inside the sheath, and so the ion and
electron number densities, 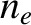 and
and 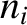 , respectively, are not
necessarily equal to one another.
, respectively, are not
necessarily equal to one another.
Consider the ion fluid. Let us assume that the mean ion velocity, 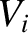 ,
is much greater than the ion thermal velocity,
,
is much greater than the ion thermal velocity,
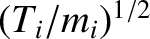 . Because,
as will become apparent,
. Because,
as will become apparent,
 , this ordering necessarily implies
that
, this ordering necessarily implies
that
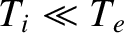 : that is, that the ions are
cold with respect to the electrons. It turns out that plasmas in the
immediate vicinity of solid walls often have comparatively cold ions, so our ordering assumption
is fairly reasonable. In the cold ion limit, the pressure term in Equation (4.243)
is negligible, and the equation can be integrated to
give
: that is, that the ions are
cold with respect to the electrons. It turns out that plasmas in the
immediate vicinity of solid walls often have comparatively cold ions, so our ordering assumption
is fairly reasonable. In the cold ion limit, the pressure term in Equation (4.243)
is negligible, and the equation can be integrated to
give
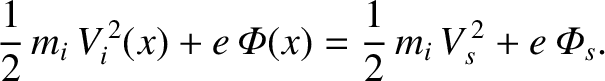 |
(4.245) |
Here, 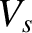 and
and
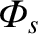 are the mean ion velocity and electrostatic
potential, respectively, at the edge of the sheath (i.e.,
are the mean ion velocity and electrostatic
potential, respectively, at the edge of the sheath (i.e.,
 ).
Now, ion fluid continuity requires that
).
Now, ion fluid continuity requires that
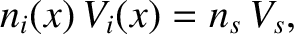 |
(4.246) |
where 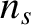 is the ion number density at the sheath boundary. Incidentally, because we
expect quasi-neutrality to hold in the plasma outside the sheath, the electron number density
at the edge of the sheath must also be
is the ion number density at the sheath boundary. Incidentally, because we
expect quasi-neutrality to hold in the plasma outside the sheath, the electron number density
at the edge of the sheath must also be 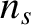 (assuming singly-charged
ions). The previous two equations can be combined to give
(assuming singly-charged
ions). The previous two equations can be combined to give
Consider the electron fluid. Let us assume that the mean electron
velocity,  , is much less than the electron thermal
velocity,
, is much less than the electron thermal
velocity,
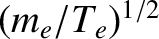 . In fact, this must be the case, otherwise,
the electron flux to the wall would greatly exceed the ion flux.
Now, if the electron fluid is essentially stationary then the left-hand side of
Equation (4.244) is negligible, and the equation can be integrated to
give
. In fact, this must be the case, otherwise,
the electron flux to the wall would greatly exceed the ion flux.
Now, if the electron fluid is essentially stationary then the left-hand side of
Equation (4.244) is negligible, and the equation can be integrated to
give
![$\displaystyle n_e = n_s\,\exp\left[\frac{e\,({\mit\Phi}-{\mit\Phi}_s)}{T_e}\right].$](img1573.png) |
(4.249) |
Here, we have made use of the fact that 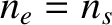 at
the edge of the sheath.
at
the edge of the sheath.
Poisson's equation is written
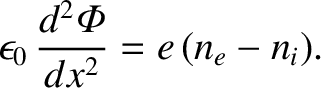 |
(4.250) |
It follows that
![$\displaystyle \epsilon_0\,\frac{d^2{\mit\Phi}}{dx^2}= e\,n_s\left(\exp\left[\fr...
...1- \frac{2\,e}{m_i\,V_s^{\,2}}\,({\mit\Phi}-{\mit\Phi}_s)\right]^{-1/2}\right).$](img1576.png) |
(4.251) |
Let
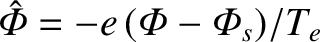 ,
,
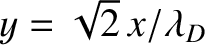 , and
, and
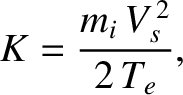 |
(4.252) |
where
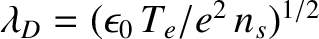 is the Debye length. Equation (4.251) transforms to
is the Debye length. Equation (4.251) transforms to
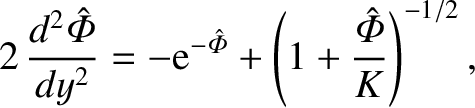 |
(4.253) |
subject to the boundary condition
 as
as
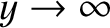 .
Multiplying through by
.
Multiplying through by
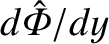 , integrating with respect to
, integrating with respect to  , and making use of the
boundary condition, we obtain
, and making use of the
boundary condition, we obtain
![$\displaystyle \left(\frac{d\skew{3}\hat{\mit\Phi}}{dy}\right)^2 = {\rm e}^{-\sk...
...}-1+ 2\,K\left[
\left(1+\frac{\skew{3}\hat{\mit\Phi}}{K}\right)^{1/2}-1\right].$](img1585.png) |
(4.254) |
Unfortunately, the previous equation is highly nonlinear, and can only be solved numerically.
However, it is not necessary to attempt this to see that
a physical solution can only exist
if the right-hand side of the equation is positive for all 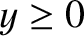 . Consider the
limit
. Consider the
limit
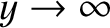 . It follows from the boundary condition that
. It follows from the boundary condition that
 . Expanding
the right-hand side of Equation (4.254) in powers of
. Expanding
the right-hand side of Equation (4.254) in powers of
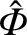 , we find that the zeroth- and first-order terms cancel, and we are left with
, we find that the zeroth- and first-order terms cancel, and we are left with
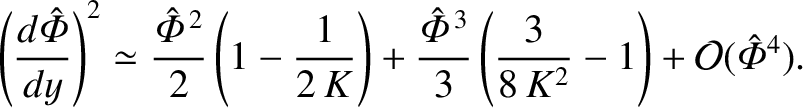 |
(4.255) |
Now, the purpose of the sheath is to shield the plasma from the wall
potential. It can be seen, from the previous expression, that the physical
solution with
maximum possible shielding corresponds to 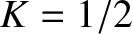 , because this
choice eliminates the first term on the right-hand side (thereby making
, because this
choice eliminates the first term on the right-hand side (thereby making
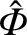 as small as possible at large
as small as possible at large  ) leaving the much smaller,
but positive (note that
) leaving the much smaller,
but positive (note that
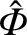 is positive), second term.
Hence, we conclude that
is positive), second term.
Hence, we conclude that
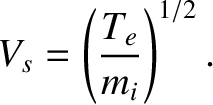 |
(4.256) |
This result is known as the Bohm sheath criterion.
It is a somewhat surprising result, because it indicates that
ions at the edge of the sheath are already moving toward the wall at a
considerable velocity. Of course, the ions are further accelerated
as they pass through the sheath. Because the ions are presumably at
rest in the interior of the plasma, it is clear that there
must exist a region sandwiched between the sheath and the main plasma
in which the ions are accelerated from rest to the Bohm velocity,
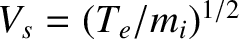 . This region is called the pre-sheath,
and is both quasi-neutral and much wider than the sheath (the actual
width depends on the nature of the ion source).
. This region is called the pre-sheath,
and is both quasi-neutral and much wider than the sheath (the actual
width depends on the nature of the ion source).
The ion current density at the wall is
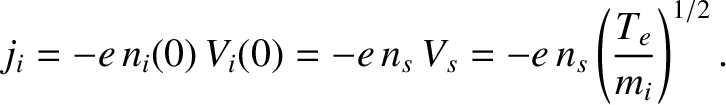 |
(4.257) |
This current density is negative because the ions are moving in the negative  -direction. What about the electron current density? Well, the
number density of electrons at the wall is
-direction. What about the electron current density? Well, the
number density of electrons at the wall is
![$n_e(0) = n_s\,\exp[\,e\,({\mit\Phi}_w-{\mit\Phi}_s)/T_e)]$](img1593.png) , where
, where
 is the wall potential. Let us assume
that the electrons have a Maxwellian velocity distribution peaked at
zero velocity (because the electron fluid velocity is much less than the
electron thermal velocity). It follows that half of the electrons at
is the wall potential. Let us assume
that the electrons have a Maxwellian velocity distribution peaked at
zero velocity (because the electron fluid velocity is much less than the
electron thermal velocity). It follows that half of the electrons at  are moving in
the negative-
are moving in
the negative- direction, and half in the positive-
direction, and half in the positive- direction.
Of course, the former electrons hit the wall, and thereby constitute an electron
current to the wall. This current is
direction.
Of course, the former electrons hit the wall, and thereby constitute an electron
current to the wall. This current is
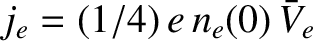 , where
the
, where
the 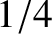 comes from averaging over solid angle, and
comes from averaging over solid angle, and
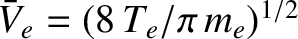 is the mean electron speed corresponding to a
Maxwellian velocity distribution (Reif 1965). Thus, the electron current density at the wall
is
is the mean electron speed corresponding to a
Maxwellian velocity distribution (Reif 1965). Thus, the electron current density at the wall
is
![$\displaystyle j_e= e\,n_s\,\left(\frac{T_e}{2\pi\,m_e}\right)^{1/2} \exp\left[\frac{e\,({\mit\Phi}_w-{\mit\Phi}_s)}{T_e}\right].$](img1598.png) |
(4.258) |
In order to replace the electrons lost to the wall, the electrons must have a mean velocity
![$\displaystyle V_{e\,s} = \frac{j_e}{e\,n_s}= \left(\frac{T_e}{2\pi\,m_e}\right)^{1/2} \exp\left[\frac{e\,({\mit\Phi}_w-{\mit\Phi}_s)}{T_e}\right]$](img1599.png) |
(4.259) |
at the edge of the sheath. However, we previously assumed that any
electron fluid velocity was much less than the electron thermal
velocity,
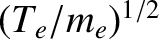 . As is clear from the previous equation,
this is only possible provided that
. As is clear from the previous equation,
this is only possible provided that
![$\displaystyle \exp\left[\frac{e\,({\mit\Phi}_w-{\mit\Phi}_s)}{T_e}\right]\ll 1:$](img1601.png) |
(4.260) |
that is, provided that the wall potential is sufficiently negative to
strongly reduce the electron number density at the wall.
The net current density at the wall is
![$\displaystyle j = e\,n_s\,\left(\frac{T_e}{m_i}\right)^{1/2}\left(\left[\frac{m...
...ght]^{1/2}\exp\left[\frac{e\,({\mit\Phi}_w-{\mit\Phi}_s)}{T_e}\right]-1\right).$](img1602.png) |
(4.261) |
Of course, we require 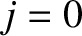 in a steady-state sheath, in order to prevent wall charging, and so we obtain
in a steady-state sheath, in order to prevent wall charging, and so we obtain
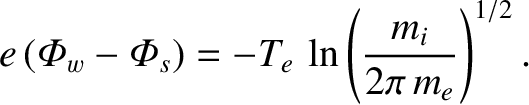 |
(4.262) |
We conclude that, in a steady-state sheath, the wall is biased negatively with respect to the
sheath edge by an amount that is proportional to the electron temperature.
Figure 4.4:
Langmuir sheath in a hydrogen plasma.
|
|
For a hydrogen plasma,
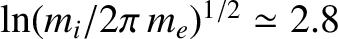 . Thus, hydrogen
ions enter the sheath with an initial energy
. Thus, hydrogen
ions enter the sheath with an initial energy
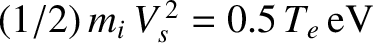 , fall through the sheath potential, and so impact the
wall with energy
, fall through the sheath potential, and so impact the
wall with energy
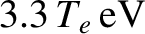 .
.
Combining Equations (4.247)–(4.249), (4.254), (4.262), and making use of the
constraint 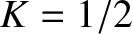 , we arrive at the following set of equations that characterize the structure of a
Langmuir sheath:
, we arrive at the following set of equations that characterize the structure of a
Langmuir sheath:
Equation (4.263) can be solved numerically, subject to the boundary condition (4.264), to
give the results summarized in Figure 4.4. The figure illustrates how the deviation from quasi-neutrality within the
sheath generates an electric potential that greatly reduces the electron number density at the wall, and also
accelerates the ions as they pass through the sheath (toward the wall).
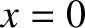 , and that the plasma occupies the
region
, and that the plasma occupies the
region  . Let us treat the ions and the electrons inside the sheath
as collisionless fluids.
The ion and electron equations of
motion are thus written
. Let us treat the ions and the electrons inside the sheath
as collisionless fluids.
The ion and electron equations of
motion are thus written
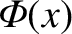 is the electrostatic potential. Moreover, we have
assumed uniform ion and electron temperatures,
is the electrostatic potential. Moreover, we have
assumed uniform ion and electron temperatures, 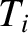 and
and  ,
respectively, for the sake of simplicity. We have also neglected any off-diagonal
terms in the ion and electron stress-tensors, because these terms are
comparatively small.
Note that quasi-neutrality
does not apply inside the sheath, and so the ion and
electron number densities,
,
respectively, for the sake of simplicity. We have also neglected any off-diagonal
terms in the ion and electron stress-tensors, because these terms are
comparatively small.
Note that quasi-neutrality
does not apply inside the sheath, and so the ion and
electron number densities, 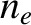 and
and 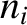 , respectively, are not
necessarily equal to one another.
, respectively, are not
necessarily equal to one another.
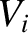 ,
is much greater than the ion thermal velocity,
,
is much greater than the ion thermal velocity,
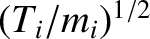 . Because,
as will become apparent,
. Because,
as will become apparent,
 , this ordering necessarily implies
that
, this ordering necessarily implies
that
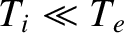 : that is, that the ions are
cold with respect to the electrons. It turns out that plasmas in the
immediate vicinity of solid walls often have comparatively cold ions, so our ordering assumption
is fairly reasonable. In the cold ion limit, the pressure term in Equation (4.243)
is negligible, and the equation can be integrated to
give
: that is, that the ions are
cold with respect to the electrons. It turns out that plasmas in the
immediate vicinity of solid walls often have comparatively cold ions, so our ordering assumption
is fairly reasonable. In the cold ion limit, the pressure term in Equation (4.243)
is negligible, and the equation can be integrated to
give
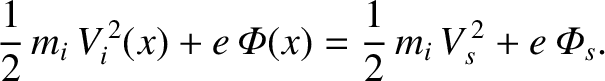
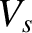 and
and
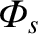 are the mean ion velocity and electrostatic
potential, respectively, at the edge of the sheath (i.e.,
are the mean ion velocity and electrostatic
potential, respectively, at the edge of the sheath (i.e.,
 ).
Now, ion fluid continuity requires that
).
Now, ion fluid continuity requires that
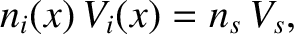
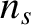 is the ion number density at the sheath boundary. Incidentally, because we
expect quasi-neutrality to hold in the plasma outside the sheath, the electron number density
at the edge of the sheath must also be
is the ion number density at the sheath boundary. Incidentally, because we
expect quasi-neutrality to hold in the plasma outside the sheath, the electron number density
at the edge of the sheath must also be 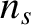 (assuming singly-charged
ions). The previous two equations can be combined to give
(assuming singly-charged
ions). The previous two equations can be combined to give
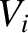
![$\displaystyle = V_s\left[1- \frac{2\,e}{m_i\,V_s^{\,2}}\,({\mit\Phi}-{\mit\Phi}_s)\right]^{1/2},$](img1569.png)
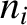
![$\displaystyle = n_s\left[1- \frac{2\,e}{m_i\,V_s^{\,2}}\,({\mit\Phi}-{\mit\Phi}_s)\right]^{-1/2}$](img1571.png)
 , is much less than the electron thermal
velocity,
, is much less than the electron thermal
velocity,
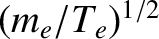 . In fact, this must be the case, otherwise,
the electron flux to the wall would greatly exceed the ion flux.
Now, if the electron fluid is essentially stationary then the left-hand side of
Equation (4.244) is negligible, and the equation can be integrated to
give
. In fact, this must be the case, otherwise,
the electron flux to the wall would greatly exceed the ion flux.
Now, if the electron fluid is essentially stationary then the left-hand side of
Equation (4.244) is negligible, and the equation can be integrated to
give
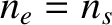 at
the edge of the sheath.
at
the edge of the sheath.
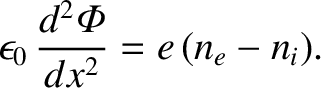
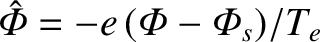 ,
,
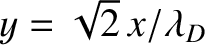 , and
, and
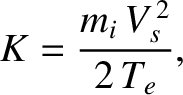
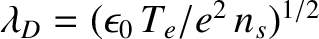 is the Debye length. Equation (4.251) transforms to
is the Debye length. Equation (4.251) transforms to
 as
as
 .
Multiplying through by
.
Multiplying through by
 , integrating with respect to
, integrating with respect to  , and making use of the
boundary condition, we obtain
Unfortunately, the previous equation is highly nonlinear, and can only be solved numerically.
However, it is not necessary to attempt this to see that
a physical solution can only exist
if the right-hand side of the equation is positive for all
, and making use of the
boundary condition, we obtain
Unfortunately, the previous equation is highly nonlinear, and can only be solved numerically.
However, it is not necessary to attempt this to see that
a physical solution can only exist
if the right-hand side of the equation is positive for all  . Consider the
limit
. Consider the
limit
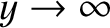 . It follows from the boundary condition that
. It follows from the boundary condition that
 . Expanding
the right-hand side of Equation (4.254) in powers of
. Expanding
the right-hand side of Equation (4.254) in powers of
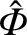 , we find that the zeroth- and first-order terms cancel, and we are left with
, we find that the zeroth- and first-order terms cancel, and we are left with
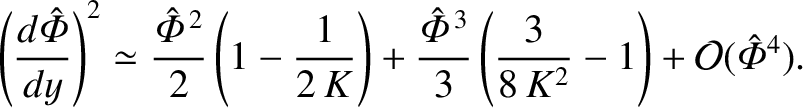
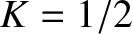 , because this
choice eliminates the first term on the right-hand side (thereby making
, because this
choice eliminates the first term on the right-hand side (thereby making
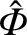 as small as possible at large
as small as possible at large  ) leaving the much smaller,
but positive (note that
) leaving the much smaller,
but positive (note that
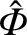 is positive), second term.
Hence, we conclude that
This result is known as the Bohm sheath criterion.
It is a somewhat surprising result, because it indicates that
ions at the edge of the sheath are already moving toward the wall at a
considerable velocity. Of course, the ions are further accelerated
as they pass through the sheath. Because the ions are presumably at
rest in the interior of the plasma, it is clear that there
must exist a region sandwiched between the sheath and the main plasma
in which the ions are accelerated from rest to the Bohm velocity,
is positive), second term.
Hence, we conclude that
This result is known as the Bohm sheath criterion.
It is a somewhat surprising result, because it indicates that
ions at the edge of the sheath are already moving toward the wall at a
considerable velocity. Of course, the ions are further accelerated
as they pass through the sheath. Because the ions are presumably at
rest in the interior of the plasma, it is clear that there
must exist a region sandwiched between the sheath and the main plasma
in which the ions are accelerated from rest to the Bohm velocity,
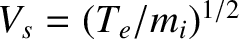 . This region is called the pre-sheath,
and is both quasi-neutral and much wider than the sheath (the actual
width depends on the nature of the ion source).
. This region is called the pre-sheath,
and is both quasi-neutral and much wider than the sheath (the actual
width depends on the nature of the ion source).
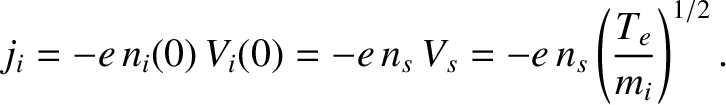
 -direction. What about the electron current density? Well, the
number density of electrons at the wall is
-direction. What about the electron current density? Well, the
number density of electrons at the wall is
![$n_e(0) = n_s\,\exp[\,e\,({\mit\Phi}_w-{\mit\Phi}_s)/T_e)]$](img1593.png) , where
, where
 is the wall potential. Let us assume
that the electrons have a Maxwellian velocity distribution peaked at
zero velocity (because the electron fluid velocity is much less than the
electron thermal velocity). It follows that half of the electrons at
is the wall potential. Let us assume
that the electrons have a Maxwellian velocity distribution peaked at
zero velocity (because the electron fluid velocity is much less than the
electron thermal velocity). It follows that half of the electrons at 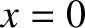 are moving in
the negative-
are moving in
the negative- direction, and half in the positive-
direction, and half in the positive- direction.
Of course, the former electrons hit the wall, and thereby constitute an electron
current to the wall. This current is
direction.
Of course, the former electrons hit the wall, and thereby constitute an electron
current to the wall. This current is
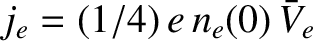 , where
the
, where
the  comes from averaging over solid angle, and
comes from averaging over solid angle, and
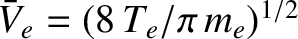 is the mean electron speed corresponding to a
Maxwellian velocity distribution (Reif 1965). Thus, the electron current density at the wall
is
is the mean electron speed corresponding to a
Maxwellian velocity distribution (Reif 1965). Thus, the electron current density at the wall
is
![$\displaystyle j_e= e\,n_s\,\left(\frac{T_e}{2\pi\,m_e}\right)^{1/2} \exp\left[\frac{e\,({\mit\Phi}_w-{\mit\Phi}_s)}{T_e}\right].$](img1598.png)
![$\displaystyle V_{e\,s} = \frac{j_e}{e\,n_s}= \left(\frac{T_e}{2\pi\,m_e}\right)^{1/2} \exp\left[\frac{e\,({\mit\Phi}_w-{\mit\Phi}_s)}{T_e}\right]$](img1599.png)
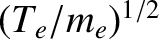 . As is clear from the previous equation,
this is only possible provided that
. As is clear from the previous equation,
this is only possible provided that
![$\displaystyle \exp\left[\frac{e\,({\mit\Phi}_w-{\mit\Phi}_s)}{T_e}\right]\ll 1:$](img1601.png)
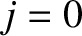 in a steady-state sheath, in order to prevent wall charging, and so we obtain
We conclude that, in a steady-state sheath, the wall is biased negatively with respect to the
sheath edge by an amount that is proportional to the electron temperature.
in a steady-state sheath, in order to prevent wall charging, and so we obtain
We conclude that, in a steady-state sheath, the wall is biased negatively with respect to the
sheath edge by an amount that is proportional to the electron temperature.
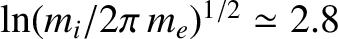 . Thus, hydrogen
ions enter the sheath with an initial energy
. Thus, hydrogen
ions enter the sheath with an initial energy
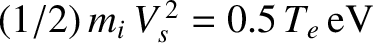 , fall through the sheath potential, and so impact the
wall with energy
, fall through the sheath potential, and so impact the
wall with energy
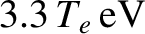 .
.
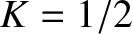 , we arrive at the following set of equations that characterize the structure of a
Langmuir sheath:
, we arrive at the following set of equations that characterize the structure of a
Langmuir sheath: