Next: Coulomb Logarithm Up: Collisions Previous: Landau Collision Operator Contents
Let
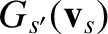 |
 |
(3.99) |
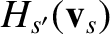 |
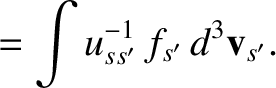 |
(3.100) |
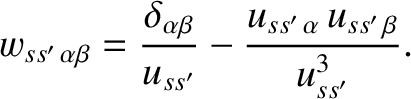 |
(3.101) |
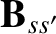 |
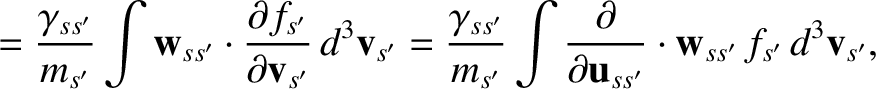 |
(3.106) |
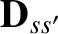 |
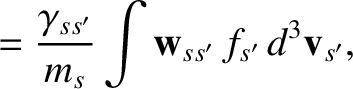 |
(3.107) |
The quantities
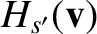 and
and
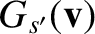 are known as Rosenbluth potentials (Rosenbluth, MacDonald, and Judd 1957), and can easily be seen to satisfy
are known as Rosenbluth potentials (Rosenbluth, MacDonald, and Judd 1957), and can easily be seen to satisfy
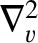 denotes a velocity-space Laplacian operator.
The former result follows because
denotes a velocity-space Laplacian operator.
The former result follows because
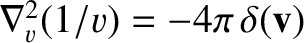 , and the
latter because
, and the
latter because
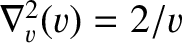 .
.
When expressed in terms of the Rosenbluth potentials, the Landau collision operator, (3.93), takes the form
where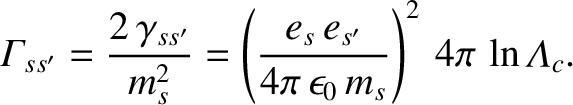 |
(3.113) |