Equations (2.35) and (2.51) can be combined to give
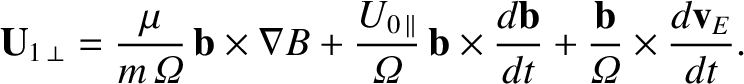 |
(2.52) |
The three terms on the right-hand side of the previous expression are conventionally
called the grad-B drift, the inertial
drift, and the polarization drift, respectively.
The grad-B drift,
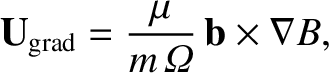 |
(2.53) |
is caused by the slight variation of the gyroradius with gyrophase as a
charged particle
rotates in a nonuniform magnetic field. The gyroradius is reduced
on the high-field side of the Larmor orbit, whereas it is increased on the
low-field side. The net result is that the orbit does not quite
close on itself. In fact, the motion consists of the conventional gyration around the magnetic
field combined with a slow drift that is perpendicular to both the
local direction of the magnetic field and the local gradient of the
field-strength.
Given that, to lowest order,
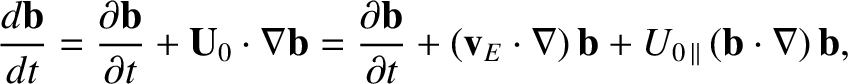 |
(2.54) |
the inertial drift can be written
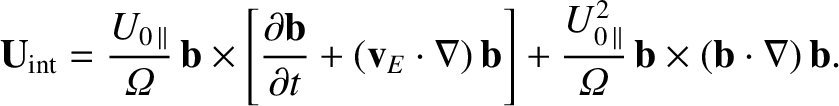 |
(2.55) |
In the important limit of stationary magnetic fields, and weak electric fields, the
previous expression is dominated by the final term,
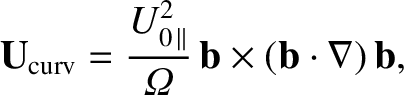 |
(2.56) |
which is called the curvature drift.
As is easily demonstrated, the quantity
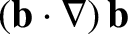 is a vector that is directed toward the center of the circle that
most closely approximates the magnetic field-line at a given point, and whose
magnitude is the inverse of the radius of this circle. Thus, the
centripetal acceleration imposed by the curvature of the magnetic field
on a charged particle following a field-line gives rise to a slow drift that is
perpendicular to both the local direction of the magnetic field and the
direction to the local center of curvature of the field.
is a vector that is directed toward the center of the circle that
most closely approximates the magnetic field-line at a given point, and whose
magnitude is the inverse of the radius of this circle. Thus, the
centripetal acceleration imposed by the curvature of the magnetic field
on a charged particle following a field-line gives rise to a slow drift that is
perpendicular to both the local direction of the magnetic field and the
direction to the local center of curvature of the field.
The polarization drift,
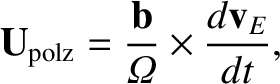 |
(2.57) |
reduces to
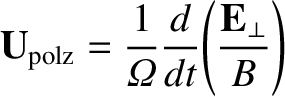 |
(2.58) |
in the limit in which the magnetic field is stationary, but the electric
field varies in time. This expression can be understood as a polarization drift
by considering what happens when we suddenly impose an electric field on a
particle at rest. The particle initially accelerates in the direction of
the electric field, but is then deflected by the magnetic force. Thereafter,
the particle undergoes conventional gyromotion combined with
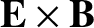 drift. The time
between the switch-on of the field and the magnetic deflection is approximately
drift. The time
between the switch-on of the field and the magnetic deflection is approximately
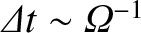 . There is no deflection if
the electric field is directed parallel to the magnetic field,
so this argument only applies to perpendicular electric fields. The initial
displacement of the particle in the direction of the field is of order
. There is no deflection if
the electric field is directed parallel to the magnetic field,
so this argument only applies to perpendicular electric fields. The initial
displacement of the particle in the direction of the field is of order
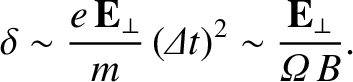 |
(2.59) |
Because
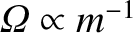 , the displacement of the
ions greatly exceeds that of the electrons.
Thus, when an electric field
is suddenly switched on in a plasma, there is an initial polarization of
the plasma medium caused, predominately, by a displacement of the ions in the direction of the
field. If the electric field, in fact, varies continuously
in time then there is a slow drift due to the constantly changing polarization of the
plasma medium. This drift is essentially the time derivative of Equation (2.59) [in other words,
Equation (2.58)].
, the displacement of the
ions greatly exceeds that of the electrons.
Thus, when an electric field
is suddenly switched on in a plasma, there is an initial polarization of
the plasma medium caused, predominately, by a displacement of the ions in the direction of the
field. If the electric field, in fact, varies continuously
in time then there is a slow drift due to the constantly changing polarization of the
plasma medium. This drift is essentially the time derivative of Equation (2.59) [in other words,
Equation (2.58)].
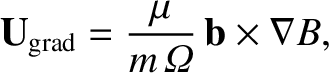
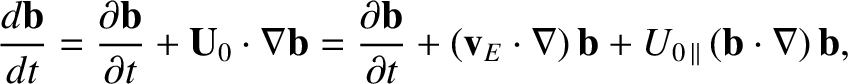
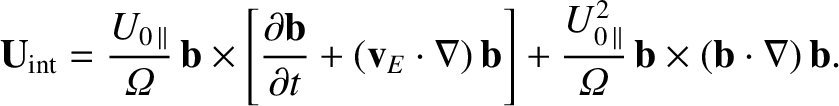
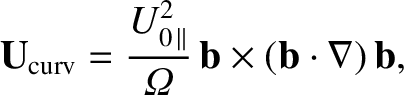
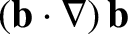 is a vector that is directed toward the center of the circle that
most closely approximates the magnetic field-line at a given point, and whose
magnitude is the inverse of the radius of this circle. Thus, the
centripetal acceleration imposed by the curvature of the magnetic field
on a charged particle following a field-line gives rise to a slow drift that is
perpendicular to both the local direction of the magnetic field and the
direction to the local center of curvature of the field.
is a vector that is directed toward the center of the circle that
most closely approximates the magnetic field-line at a given point, and whose
magnitude is the inverse of the radius of this circle. Thus, the
centripetal acceleration imposed by the curvature of the magnetic field
on a charged particle following a field-line gives rise to a slow drift that is
perpendicular to both the local direction of the magnetic field and the
direction to the local center of curvature of the field.
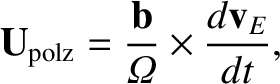
 drift. The time
between the switch-on of the field and the magnetic deflection is approximately
drift. The time
between the switch-on of the field and the magnetic deflection is approximately
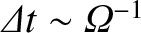 . There is no deflection if
the electric field is directed parallel to the magnetic field,
so this argument only applies to perpendicular electric fields. The initial
displacement of the particle in the direction of the field is of order
Because
. There is no deflection if
the electric field is directed parallel to the magnetic field,
so this argument only applies to perpendicular electric fields. The initial
displacement of the particle in the direction of the field is of order
Because
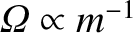 , the displacement of the
ions greatly exceeds that of the electrons.
Thus, when an electric field
is suddenly switched on in a plasma, there is an initial polarization of
the plasma medium caused, predominately, by a displacement of the ions in the direction of the
field. If the electric field, in fact, varies continuously
in time then there is a slow drift due to the constantly changing polarization of the
plasma medium. This drift is essentially the time derivative of Equation (2.59) [in other words,
Equation (2.58)].
, the displacement of the
ions greatly exceeds that of the electrons.
Thus, when an electric field
is suddenly switched on in a plasma, there is an initial polarization of
the plasma medium caused, predominately, by a displacement of the ions in the direction of the
field. If the electric field, in fact, varies continuously
in time then there is a slow drift due to the constantly changing polarization of the
plasma medium. This drift is essentially the time derivative of Equation (2.59) [in other words,
Equation (2.58)].