Next: Velocity-Space Instabilities Up: Waves in Warm Plasmas Previous: Perpendicular Wave Propagation Contents
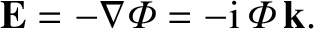 |
(7.114) |
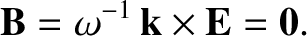 |
(7.116) |
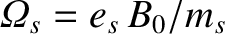 and
and
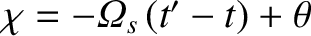 , whereas the Cartesian components of
, whereas the Cartesian components of 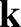 and
and 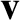 are written
are written
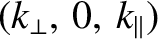 and
and
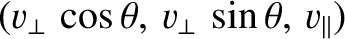 , respectively. The equilibrium magnetic field takes the form
, respectively. The equilibrium magnetic field takes the form
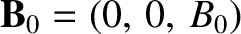 . Equations (7.115) and (7.117) can be
combined to give
After some tedious analysis, the previous expression reduces to the so-called Harris dispersion relation (Harris 1961)
. Equations (7.115) and (7.117) can be
combined to give
After some tedious analysis, the previous expression reduces to the so-called Harris dispersion relation (Harris 1961)
For Maxwellian distribution functions of the form (7.79), we can explicitly perform the velocity-space integrals in the Harris dispersion relation to give
where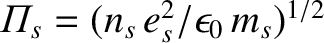 ,
,
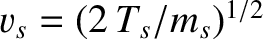 ,
,
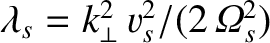 ,
and
,
and
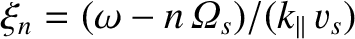 . Here, the
. Here, the 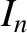 are modified Bessel functions (Abramowitz and Stegun 1965), whereas
are modified Bessel functions (Abramowitz and Stegun 1965), whereas
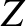 is a plasma dispersion function. (See Section 7.4.) In deriving the previous expression, use has been made of the identity (Watson 1995)
is a plasma dispersion function. (See Section 7.4.) In deriving the previous expression, use has been made of the identity (Watson 1995)
Consider electrostatic waves propagating parallel to the equilibrium magnetic field. In this case,
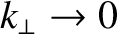 and
and
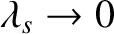 ,
so the dispersion relation (7.120) reduces to
,
so the dispersion relation (7.120) reduces to
![$\displaystyle 1 + \sum_s\frac{2\,{\mit\Pi}_s^{2}}{(k_\parallel\,v_s)^2}\left[1+\xi_0\,Z(\xi_0)\right]=0,$](img2517.png) |
(7.122) |
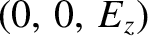 . (Recall that
. (Recall that
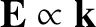 for an electrostatic wave.) It can be seen that this expression is identical to the
dispersion relation (7.97) for longitudinal plasma waves. Consider electrostatic waves propagating perpendicular to the equilibrium
magnetic field. In this case,
for an electrostatic wave.) It can be seen that this expression is identical to the
dispersion relation (7.97) for longitudinal plasma waves. Consider electrostatic waves propagating perpendicular to the equilibrium
magnetic field. In this case,
 and
and
 , so the dispersion relation (7.120) reduces to
with the eigenvector
, so the dispersion relation (7.120) reduces to
with the eigenvector
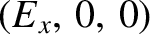 . Making use of the identity (7.121), as well as the fact that
. Making use of the identity (7.121), as well as the fact that
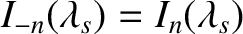 (Abramowitz and Stegun 1965), the previous expression can be rearranged to give
It can be seen that this expression is identical to the dispersion relation (7.111) for Bernstein waves. Thus, we can now appreciate that plasma waves and
Bernstein waves are merely different aspects of a more general type of electrostatic wave. This wave takes the form of a plasma wave when propagating
parallel to the equilibrium magnetic field, of a Bernstein wave when propagating perpendicular to the magnetic field, and takes an intermediate form
when propagating obliquely to the magnetic field.
(Abramowitz and Stegun 1965), the previous expression can be rearranged to give
It can be seen that this expression is identical to the dispersion relation (7.111) for Bernstein waves. Thus, we can now appreciate that plasma waves and
Bernstein waves are merely different aspects of a more general type of electrostatic wave. This wave takes the form of a plasma wave when propagating
parallel to the equilibrium magnetic field, of a Bernstein wave when propagating perpendicular to the magnetic field, and takes an intermediate form
when propagating obliquely to the magnetic field.