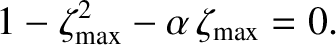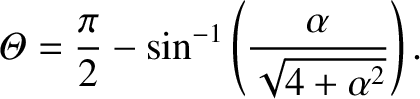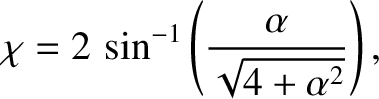Two-Body Coulomb Collisions
Consider a two-body Coulomb collision between a species- particle, with mass
particle, with mass 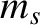 and charge
and charge 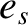 , and a species-
, and a species- particle,
with mass
particle,
with mass 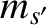 and charge
and charge 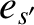 . The equations of motion of the two particles take the form
where
. The equations of motion of the two particles take the form
where
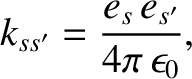 |
(3.40) |
and
 denotes a time derivative.
Here,
denotes a time derivative.
Here, 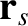 and
and
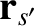 are the respective position vectors, and
are the respective position vectors, and
 is
the relative position vector.
It is easily demonstrated that
where
is
the relative position vector.
It is easily demonstrated that
where
 |
(3.43) |
is the vector position of the center of mass (which does not accelerate). Equations (3.38) and (3.39) can be combined to give a single
equation of relative motion,
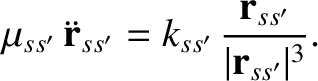 |
(3.44) |
Two relations that immediately follow from the previous equation are
where
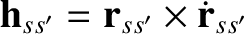 |
(3.47) |
is the conserved angular momentum per unit mass, and
 |
(3.48) |
the conserved energy.
Equation (3.47) implies that
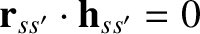 . This is the equation of a plane that passes through the origin, and whose normal is parallel
to the constant vector
. This is the equation of a plane that passes through the origin, and whose normal is parallel
to the constant vector
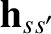 . We, therefore, conclude that the relative position vector
. We, therefore, conclude that the relative position vector 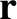 is constrained to lie in this plane,
which implies that the trajectories of both colliding particles are coplanar.
Let the plane
is constrained to lie in this plane,
which implies that the trajectories of both colliding particles are coplanar.
Let the plane
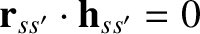 coincide with the
coincide with the 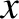 -
-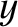 plane, so that we can write
plane, so that we can write
 . It is convenient to
define the standard plane polar coordinates
. It is convenient to
define the standard plane polar coordinates
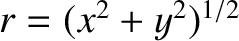 and
and
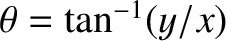 .
When expressed in terms of these coordinates, the conserved angular momentum per unit mass becomes
.
When expressed in terms of these coordinates, the conserved angular momentum per unit mass becomes
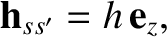 |
(3.49) |
where
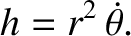 |
(3.50) |
Furthermore, the conserved energy takes the form
 |
(3.51) |
Suppose that 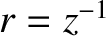 , where
, where
 and
and
 . It follows that
. It follows that
 |
(3.52) |
Hence, Equation (3.51) transforms to give
![$\displaystyle E_{ss'} = \frac{1}{2}\,\mu_{ss'}\,h^{2}\left[\left(\frac{dz}{d\theta}\right)^2 + z^{2}\right] + k_{ss'}\,z.$](img696.png) |
(3.53) |
It is convenient to define the relative velocity at large distances,
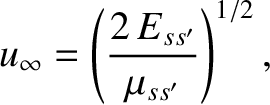 |
(3.54) |
as well as the impact parameter,
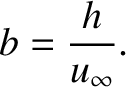 |
(3.55) |
The latter parameter is simply the distance of closest approach of the two particles in the situation in which there is no Coulomb force acting between them,
and they, consequently, move in straight-lines. (See Figure 3.1.) The previous three equations can be combined to give
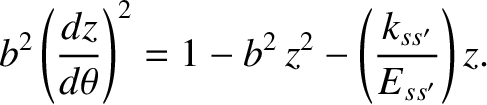 |
(3.56) |
Figure 3.1:
A two-body Coulomb collision.
|
|
Figure 3.1 shows the collision in a frame of reference in which the species- particle remains stationary at the origin,
particle remains stationary at the origin,  ,
whereas the species-
,
whereas the species- particle traces out the path
particle traces out the path  . Point
. Point  corresponds to the closest approach of the
two particles. It follows, by symmetry (because Coulomb collisions are reversible), that the angles
corresponds to the closest approach of the
two particles. It follows, by symmetry (because Coulomb collisions are reversible), that the angles 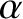 and
and 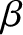 shown in the figure are equal to one another. Hence, we deduce that
shown in the figure are equal to one another. Hence, we deduce that
 |
(3.57) |
Here, 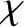 is the angle through which the path of the species-
is the angle through which the path of the species- (or the species-
(or the species- particle) is deviated as a consequence of the collision,
whereas
particle) is deviated as a consequence of the collision,
whereas
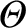 is the angle through which the relative position vector,
is the angle through which the relative position vector,
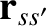 , rotates as the species-
, rotates as the species- particle
moves from point
particle
moves from point 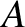 (which is assumed to be infinity far from point
(which is assumed to be infinity far from point 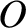 ) to point
) to point  . Suppose that point
. Suppose that point 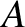 corresponds to
corresponds to 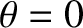 . It follows that
. It follows that
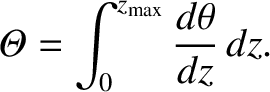 |
(3.58) |
Here,
 , where
, where
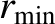 is the distance of closest approach.
Now, by symmetry,
is the distance of closest approach.
Now, by symmetry,
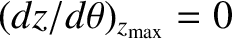 , so Equation (3.56) implies that
, so Equation (3.56) implies that
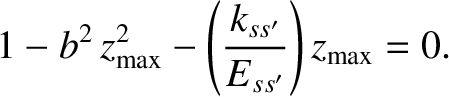 |
(3.59) |
Combining Equations (3.56) and (3.58), we obtain
 |
(3.60) |
where
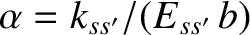 , and
, and
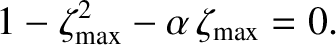 |
(3.61) |
Integration (Speigel, Liu, and Lipschutz 1999) yields
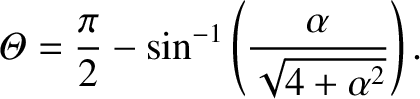 |
(3.62) |
Hence, from Equation (3.57), we get
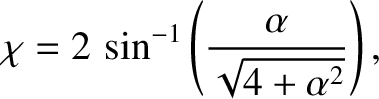 |
(3.63) |
which can be rearranged to give
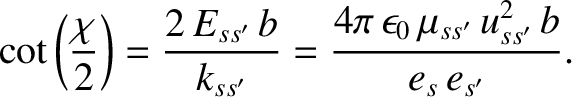 |
(3.64) |
Note that the analysis in this section tacitly assumes that Coulomb collisions are not significantly modified by
any magnetic field that might pervade the plasma. This assumption is justified provided that the particle gyroradii are all much
larger than the Debye length.
 particle, with mass
particle, with mass 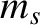 and charge
and charge 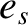 , and a species-
, and a species- particle,
with mass
particle,
with mass 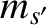 and charge
and charge 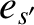 . The equations of motion of the two particles take the form
where
. The equations of motion of the two particles take the form
where
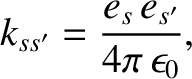
 denotes a time derivative.
Here,
denotes a time derivative.
Here, 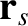 and
and
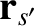 are the respective position vectors, and
are the respective position vectors, and
 is
the relative position vector.
It is easily demonstrated that
is
the relative position vector.
It is easily demonstrated that
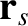

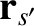
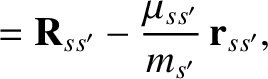


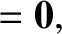
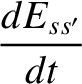
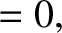

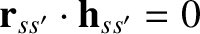 . This is the equation of a plane that passes through the origin, and whose normal is parallel
to the constant vector
. This is the equation of a plane that passes through the origin, and whose normal is parallel
to the constant vector
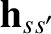 . We, therefore, conclude that the relative position vector
. We, therefore, conclude that the relative position vector 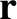 is constrained to lie in this plane,
which implies that the trajectories of both colliding particles are coplanar.
Let the plane
is constrained to lie in this plane,
which implies that the trajectories of both colliding particles are coplanar.
Let the plane
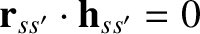 coincide with the
coincide with the 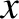 -
-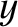 plane, so that we can write
plane, so that we can write
 . It is convenient to
define the standard plane polar coordinates
. It is convenient to
define the standard plane polar coordinates
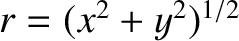 and
and
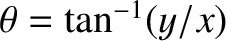 .
When expressed in terms of these coordinates, the conserved angular momentum per unit mass becomes
.
When expressed in terms of these coordinates, the conserved angular momentum per unit mass becomes
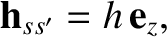
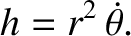
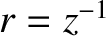 , where
, where
 and
and
 . It follows that
. It follows that

![$\displaystyle E_{ss'} = \frac{1}{2}\,\mu_{ss'}\,h^{2}\left[\left(\frac{dz}{d\theta}\right)^2 + z^{2}\right] + k_{ss'}\,z.$](img696.png)
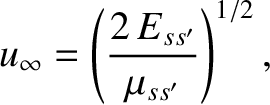
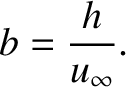
 particle remains stationary at the origin,
particle remains stationary at the origin, 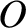 ,
whereas the species-
,
whereas the species- particle traces out the path
particle traces out the path 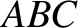 . Point
. Point  corresponds to the closest approach of the
two particles. It follows, by symmetry (because Coulomb collisions are reversible), that the angles
corresponds to the closest approach of the
two particles. It follows, by symmetry (because Coulomb collisions are reversible), that the angles 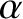 and
and 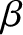 shown in the figure are equal to one another. Hence, we deduce that
shown in the figure are equal to one another. Hence, we deduce that
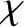 is the angle through which the path of the species-
is the angle through which the path of the species- (or the species-
(or the species- particle) is deviated as a consequence of the collision,
whereas
particle) is deviated as a consequence of the collision,
whereas
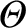 is the angle through which the relative position vector,
is the angle through which the relative position vector,
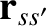 , rotates as the species-
, rotates as the species- particle
moves from point
particle
moves from point 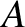 (which is assumed to be infinity far from point
(which is assumed to be infinity far from point 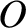 ) to point
) to point  . Suppose that point
. Suppose that point 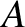 corresponds to
corresponds to 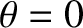 . It follows that
Here,
. It follows that
Here,
 , where
, where
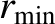 is the distance of closest approach.
Now, by symmetry,
is the distance of closest approach.
Now, by symmetry,
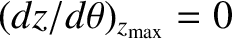 , so Equation (3.56) implies that
, so Equation (3.56) implies that
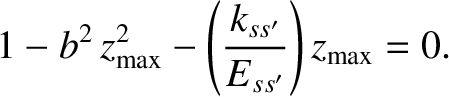

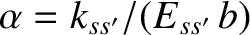 , and
, and