Next: Motion in Uniform Fields Up: Charged Particle Motion Previous: Charged Particle Motion Contents
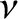 , greatly exceeds the
gyrofrequency,
, greatly exceeds the
gyrofrequency,
 . In this case, the particles are scattered
after executing only a small fraction of a gyro-orbit, and, therefore, still move
essentially in straight-lines between collisions. The situation of primary
interest in this chapter is that of a magnetized, but collisionless
(i.e.,
. In this case, the particles are scattered
after executing only a small fraction of a gyro-orbit, and, therefore, still move
essentially in straight-lines between collisions. The situation of primary
interest in this chapter is that of a magnetized, but collisionless
(i.e.,
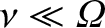 ), plasma, in which the gyroradius,
), plasma, in which the gyroradius,
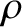 , is much smaller than the typical variation lengthscale,
, is much smaller than the typical variation lengthscale, 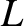 , of the
, of the
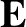 and
and 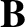 fields, and the gyroperiod,
fields, and the gyroperiod,
 , is
much less than the typical timescale,
, is
much less than the typical timescale,  , on which these fields change.
In such a plasma, we expect the motion of the constituent particles to consist
of a rapid gyration perpendicular to
magnetic field-lines, combined with free streaming parallel
to the field-lines. We are particularly interested in calculating how
this motion is affected by the spatial and temporal gradients in the
, on which these fields change.
In such a plasma, we expect the motion of the constituent particles to consist
of a rapid gyration perpendicular to
magnetic field-lines, combined with free streaming parallel
to the field-lines. We are particularly interested in calculating how
this motion is affected by the spatial and temporal gradients in the
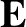 and
and 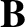 fields. In general, the motion of charged particles
in spatially and temporally nonuniform electromagnetic
fields is extremely complicated. However,
we hope to considerably simplify this motion by exploiting the
assumed smallness of the parameters
fields. In general, the motion of charged particles
in spatially and temporally nonuniform electromagnetic
fields is extremely complicated. However,
we hope to considerably simplify this motion by exploiting the
assumed smallness of the parameters 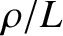 and
and
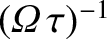 .
What we are essentially trying to understand, in this chapter, is how the
magnetic confinement of a collisionless plasma works
at an individual particle level.
The type of collisionless, magnetized plasma investigated here occurs primarily in magnetic fusion and space plasma physics
contexts.
.
What we are essentially trying to understand, in this chapter, is how the
magnetic confinement of a collisionless plasma works
at an individual particle level.
The type of collisionless, magnetized plasma investigated here occurs primarily in magnetic fusion and space plasma physics
contexts.