Next: Flux Freezing Up: Magnetohydrodynamic Fluids Previous: Introduction Contents
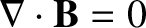 , provided that this relation is
presumed to hold initially. Furthermore, the assumption of
quasi-neutrality renders the Poisson-Maxwell equation,
, provided that this relation is
presumed to hold initially. Furthermore, the assumption of
quasi-neutrality renders the Poisson-Maxwell equation,
 , redundant.
, redundant.
Equations (8.2) and (8.7) can be combined to give the MHD equation of motion:
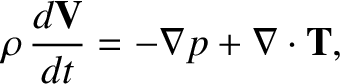 |
(8.9) |
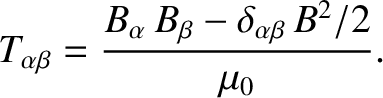 |
(8.10) |
Suppose that the magnetic field is approximately uniform, and
directed along the 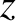 -axis. In this case, the previous equation of
motion reduces to
-axis. In this case, the previous equation of
motion reduces to
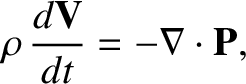 |
(8.11) |
![$\displaystyle {\bf P} = \left(\begin{array}{ccc}
p + B^{2}/2\,\mu_0, & 0, &0\\ ...
... &p + B^{2}/2\,\mu_0,& 0\\ [0.5ex]
0,&0,& p - B^{2}/2\,\mu_0\end{array}\right).$](img2688.png) |
(8.12) |
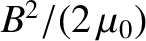 , in directions perpendicular to the magnetic field,
and decreases the plasma pressure, by the same amount, in the
parallel direction. Thus, the magnetic field gives rise to
a magnetic pressure,
, in directions perpendicular to the magnetic field,
and decreases the plasma pressure, by the same amount, in the
parallel direction. Thus, the magnetic field gives rise to
a magnetic pressure,
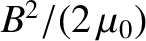 , acting perpendicular to field-lines,
and a magnetic tension,
, acting perpendicular to field-lines,
and a magnetic tension,
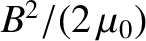 , acting
along field-lines.
Because, as will become apparent in the next section, the plasma is tied to magnetic field-lines,
it follows that magnetic field-lines embedded in an
MHD plasma act rather like
mutually repulsive elastic bands.
, acting
along field-lines.
Because, as will become apparent in the next section, the plasma is tied to magnetic field-lines,
it follows that magnetic field-lines embedded in an
MHD plasma act rather like
mutually repulsive elastic bands.