Next: Plasma Beta
Up: Introduction
Previous: Collisions
A magnetized plasma is one in which the ambient magnetic field,
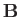 , is strong enough to significantly alter particle
trajectories. In particular,
magnetized plasmas are highly anisotropic, responding differently to
forces that are parallel and perpendicular to the direction
of
, is strong enough to significantly alter particle
trajectories. In particular,
magnetized plasmas are highly anisotropic, responding differently to
forces that are parallel and perpendicular to the direction
of 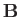 . Incidentally, a magnetized plasma moving with
mean velocity
. Incidentally, a magnetized plasma moving with
mean velocity 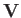 contains an electric field
contains an electric field
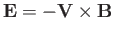 that is not affected
by Debye shielding. Of course, the electric
field is essentially zero in the rest frame of the plasma.
that is not affected
by Debye shielding. Of course, the electric
field is essentially zero in the rest frame of the plasma.
As is well known, charged particles respond to the Lorentz force,
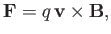 |
(1.28) |
by freely streaming in the direction of 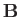 , while executing
circular Larmor orbits, or gyro-orbits, in the plane perpendicular to
, while executing
circular Larmor orbits, or gyro-orbits, in the plane perpendicular to 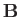 (Fitzpatrick 2008).
As the field-strength increases, the resulting helical orbits become more
tightly wound, effectively tying particles to magnetic field-lines.
(Fitzpatrick 2008).
As the field-strength increases, the resulting helical orbits become more
tightly wound, effectively tying particles to magnetic field-lines.
The typical Larmor radius, or gyroradius, of a charged particle
gyrating in a
magnetic field is given by
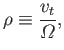 |
(1.29) |
where
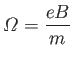 |
(1.30) |
is the cyclotron frequency, or gyrofrequency, associated with the
gyration. As usual, there is a distinct gyroradius for each species.
When species temperatures are comparable, the electron gyroradius is
distinctly smaller than the ion gyroradius:
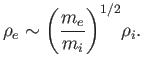 |
(1.31) |
A plasma system, or process, is said to be magnetized if its
characteristic lengthscale, 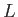 , is large compared to the gyroradius.
In the opposite limit,
, is large compared to the gyroradius.
In the opposite limit, 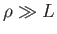 , charged particles have essentially
straight-line trajectories. Thus, the ability of the magnetic field to
significantly affect particle trajectories is measured by the
magnetization parameter,
, charged particles have essentially
straight-line trajectories. Thus, the ability of the magnetic field to
significantly affect particle trajectories is measured by the
magnetization parameter,
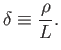 |
(1.32) |
There are some cases of interest in which the electrons are magnetized, but the
ions are not. However, a ``magnetized'' plasma conventionally refers to
one in which both species are magnetized. This state is generally achieved
when
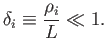 |
(1.33) |



Next: Plasma Beta
Up: Introduction
Previous: Collisions
Richard Fitzpatrick
2016-01-23
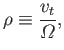
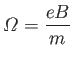
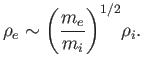
![]() , is large compared to the gyroradius.
In the opposite limit,
, is large compared to the gyroradius.
In the opposite limit, ![]() , charged particles have essentially
straight-line trajectories. Thus, the ability of the magnetic field to
significantly affect particle trajectories is measured by the
magnetization parameter,
, charged particles have essentially
straight-line trajectories. Thus, the ability of the magnetic field to
significantly affect particle trajectories is measured by the
magnetization parameter,