where
whereas any time variation generates a polarization current whose density is
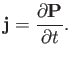
Consider an electromagnetic wave propagating through a quasi-neutral, linear, dielectric medium. Assuming a common
where
demonstrate that
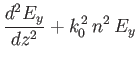 |
||
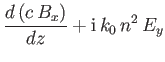 |
where
demonstrate that
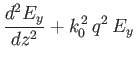 |
||
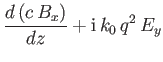 |
where
and
Show that the WKB solutions take the form
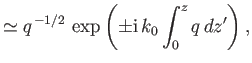 |
||
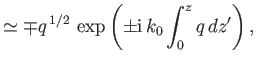 |
and that the criterion for these solutions to be valid is
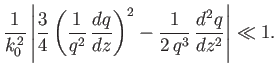
demonstrate that
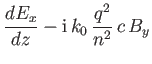 |
||
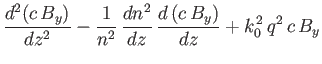 |
where
and
Show that the WKB solutions take the form
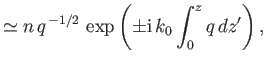 |
||
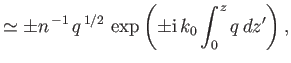 |
and that the criterion for these solutions to be valid is
![$\displaystyle \frac{1}{k_0^{\,2}}\left\vert\frac{3}{4}\left(\frac{1}{q^2}\,\fra...
...2n}{dz^2}-2\,\left(\frac{1}{n}\,\frac{dn}{dz}\right)^2\right]\right\vert\ll 1.
$](img2223.png)
- Demonstrate that
![$\displaystyle h(\omega) = \int_0^{z_0(\omega)}\frac{\omega}{\left[\omega^2- {\mit\Pi}_e^{\,2}(z)\right]^{\,1/2}}\,dz,
$](img2227.png)
where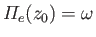 .
.
- Show that if
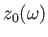 is a monotonically increasing function of
is a monotonically increasing function of 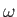 then the previous integral can be inverted to
give
then the previous integral can be inverted to
give
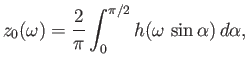
or, equivalently,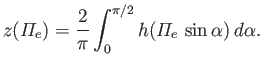
(Hint: This is a form of Abel inversion. See Budden 1985.) - Demonstrate that if
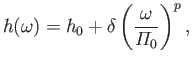
where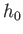 ,
, 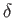 , and
, and
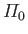 are positive constants, then
are positive constants, then
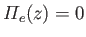 for
for 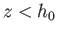 , and
, and
![$\displaystyle {\mit\Pi}_e(z) =\left[\frac{\pi\,{\mit\Gamma}(1+p)}{{\mit\Gamma}(...
.../2)}\right]^{1/p} \frac{{\mit\Pi}_0}{2}\left(\frac{z-h_0}{\delta}\right)^{1/p}
$](img2237.png)
for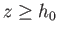 . Here,
. Here,
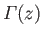 is a Gamma function (Abramowitz and Stegun 1965a).
is a Gamma function (Abramowitz and Stegun 1965a).
- A point transmitter sends up a wave packet at an angle
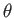 to the vertical. Show that the packet returns to Earth a
distance
to the vertical. Show that the packet returns to Earth a
distance
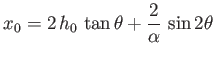
from the transmitter. Demonstrate that if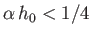 then for some values of
then for some values of 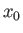 the previous equation is satisfied
by three different values of
the previous equation is satisfied
by three different values of 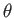 . In other words, wave packets can travel from the transmitter to the receiver via one of
three different paths. Show that the critical case
. In other words, wave packets can travel from the transmitter to the receiver via one of
three different paths. Show that the critical case
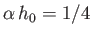 corresponds to
corresponds to
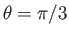 and
and
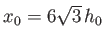 .
.
- A point
radio transmitter emits a pulse of radio waves uniformly in all directions. Show that the pulse first returns to the Earth a
distance
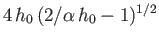 from the transmitter, provided that
from the transmitter, provided that
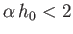 .
.