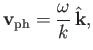Next: Cold-Plasma Dielectric Permittivity
Up: Waves in Cold Plasmas
Previous: Introduction
Plane Waves in Homogeneous Plasmas
The propagation of small amplitude plasma waves is described by linearized equations
that are obtained by expanding the plasma equations of motion in powers
of the wave amplitude, and then neglecting terms of order higher than unity.
Consider a homogeneous, magnetized, quasi-neutral plasma, consisting of equal
numbers of electrons and ions, in which the mean velocities of both plasma species are zero.
It follows that
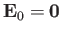 , and
, and
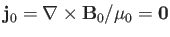 , where the subscript 0
denotes an equilibrium quantity.
In a homogeneous medium, the
general solution of a system of linear equations can be constructed as
a superposition of plane wave solutions of the form (Fitzpatrick 2013)
, where the subscript 0
denotes an equilibrium quantity.
In a homogeneous medium, the
general solution of a system of linear equations can be constructed as
a superposition of plane wave solutions of the form (Fitzpatrick 2013)
![$\displaystyle {\bf E} ({\bf r}, t) = {\bf E}_{\bf k} \,\exp[\,{\rm i}\,({\bf k} \cdot{\bf r} - \omega\, t)],$](img1686.png) |
(5.1) |
with analogous expressions for
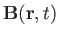 and
and
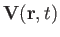 .
Here,
.
Here, 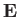 ,
, 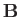 , and
, and 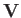 are the perturbed electric field, magnetic field, and
plasma center-of-mass velocity, respectively.
The
surfaces of constant phase,
are the perturbed electric field, magnetic field, and
plasma center-of-mass velocity, respectively.
The
surfaces of constant phase,
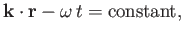 |
(5.2) |
are planes perpendicular to 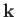 , traveling at the velocity
, traveling at the velocity
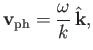 |
(5.3) |
where
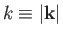 , and
, and
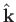 is a unit vector
pointing in the direction of
is a unit vector
pointing in the direction of 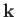 . Here,
. Here,
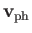 is termed the phase-velocity of the wave (Fitzpatrick 2013).
Henceforth, for ease of notation, we shall omit
the subscript
is termed the phase-velocity of the wave (Fitzpatrick 2013).
Henceforth, for ease of notation, we shall omit
the subscript 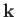 from field variables.
from field variables.
Substitution of the plane-wave solution (5.1) into Maxwell's equations yields
where
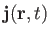 is the perturbed current density.
In linear theory, the current is related to the electric field via
is the perturbed current density.
In linear theory, the current is related to the electric field via
where the electrical conductivity tensor,
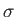 , is a
function of both
, is a
function of both 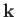 and
and 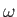 . In the presence of a non-zero equilibrium
magnetic field, this tensor is anisotropic in nature.
. In the presence of a non-zero equilibrium
magnetic field, this tensor is anisotropic in nature.
Substitution of Equation (5.6) into Equation (5.4) yields
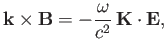 |
(5.7) |
where
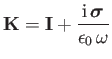 |
(5.8) |
is termed the dielectric permittivity tensor.
Here, 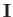 is the identity tensor. Eliminating the
magnetic field between Equations (5.5) and (5.7), we obtain
is the identity tensor. Eliminating the
magnetic field between Equations (5.5) and (5.7), we obtain
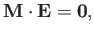 |
(5.9) |
where
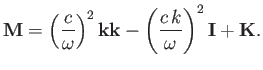 |
(5.10) |
The solubility condition for Equation (5.9),
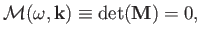 |
(5.11) |
is called the dispersion relation, and
relates the wave angular frequency, 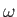 , to the wavevector,
, to the wavevector, 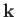 .
Also, as the name
``dispersion relation'' suggests, this relation allows us to determine the rate at which the
different Fourier components of a wave pulse disperse due to
the variation of their phase-velocity with frequency (Fitzpatrick 2013).
.
Also, as the name
``dispersion relation'' suggests, this relation allows us to determine the rate at which the
different Fourier components of a wave pulse disperse due to
the variation of their phase-velocity with frequency (Fitzpatrick 2013).



Next: Cold-Plasma Dielectric Permittivity
Up: Waves in Cold Plasmas
Previous: Introduction
Richard Fitzpatrick
2016-01-23
![]() , and
, and
![]() , where the subscript 0
denotes an equilibrium quantity.
In a homogeneous medium, the
general solution of a system of linear equations can be constructed as
a superposition of plane wave solutions of the form (Fitzpatrick 2013)
, where the subscript 0
denotes an equilibrium quantity.
In a homogeneous medium, the
general solution of a system of linear equations can be constructed as
a superposition of plane wave solutions of the form (Fitzpatrick 2013)