


Next: Motion in Oscillating Fields
Up: Charged Particle Motion
Previous: Second Adiabatic Invariant
Third Adiabatic Invariant
It is clear, by now, that there is an adiabatic invariant associated
with every periodic motion of a charged particle in
an electromagnetic field.
We have just demonstrated that, as a consequence of  -conservation,
the drift orbit of a charged particle precessing around the Earth is approximately
closed, despite the fact that the Earth's magnetic field is non-axisymmetric.
Thus, there must be a third adiabatic invariant associated with the
precession of particles around the Earth. Just as we can define a
guiding center associated with a particle's gyromotion around field-lines,
we can also define a bounce center associated with a particle's bouncing
motion between mirror points. The bounce center lies on the equatorial plane, and
orbits the Earth once every drift period,
-conservation,
the drift orbit of a charged particle precessing around the Earth is approximately
closed, despite the fact that the Earth's magnetic field is non-axisymmetric.
Thus, there must be a third adiabatic invariant associated with the
precession of particles around the Earth. Just as we can define a
guiding center associated with a particle's gyromotion around field-lines,
we can also define a bounce center associated with a particle's bouncing
motion between mirror points. The bounce center lies on the equatorial plane, and
orbits the Earth once every drift period, 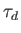 .
We can write the third adiabatic invariant as
.
We can write the third adiabatic invariant as
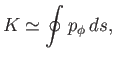 |
(2.119) |
where the path of integration is the trajectory of the bounce center around
the Earth. Incidentally, the drift trajectory
effectively collapses onto the trajectory of the bounce center
in the limit that
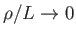 , because all
of the particle's gyromotion and bounce motion averages to zero.
Now,
, because all
of the particle's gyromotion and bounce motion averages to zero.
Now,
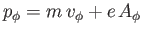 is dominated by its second term,
as the drift velocity
is dominated by its second term,
as the drift velocity 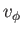 is very small. Thus,
is very small. Thus,
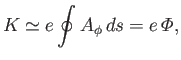 |
(2.120) |
where
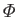 is the total magnetic flux enclosed by the drift
trajectory (that is, the flux enclosed by the orbit of the bounce center
around the Earth). The previous ``proof'' of the invariance of
is the total magnetic flux enclosed by the drift
trajectory (that is, the flux enclosed by the orbit of the bounce center
around the Earth). The previous ``proof'' of the invariance of
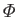 is, again, not particularly rigorous. In fact, the invariance of
is, again, not particularly rigorous. In fact, the invariance of
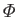 was first demonstrated rigorously by Northrop
(Northrop 1963). Of course,
was first demonstrated rigorously by Northrop
(Northrop 1963). Of course,
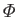 is only a constant
of the motion for particles trapped in the inner magnetosphere provided the
magnetospheric magnetic field varies on timescales that are much longer than
the drift period,
is only a constant
of the motion for particles trapped in the inner magnetosphere provided the
magnetospheric magnetic field varies on timescales that are much longer than
the drift period, 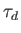 . Because the drift period for MeV energy
protons and electrons is of order an hour, this is only likely
to be the case when the magnetosphere is relatively quiescent (in other words,
when there are no geomagnetic storms in progress).
. Because the drift period for MeV energy
protons and electrons is of order an hour, this is only likely
to be the case when the magnetosphere is relatively quiescent (in other words,
when there are no geomagnetic storms in progress).
The invariance of
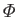 has interesting consequences for charged
particle dynamics in the Earth's inner magnetosphere. Suppose, for instance,
that the
strength of the solar wind were to increase slowly (that is, on timescales
significantly longer than the drift period), thereby, compressing the Earth's
magnetic field. The invariance of
has interesting consequences for charged
particle dynamics in the Earth's inner magnetosphere. Suppose, for instance,
that the
strength of the solar wind were to increase slowly (that is, on timescales
significantly longer than the drift period), thereby, compressing the Earth's
magnetic field. The invariance of
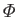 would cause the charged particles
that constitute the Van Allen belts
to move radially inwards, toward the Earth, in order
to conserve the magnetic flux enclosed by their drift orbits. Likewise, a
slow decrease in the strength of the solar wind would cause an outward radial motion
of the Van Allen belts.
would cause the charged particles
that constitute the Van Allen belts
to move radially inwards, toward the Earth, in order
to conserve the magnetic flux enclosed by their drift orbits. Likewise, a
slow decrease in the strength of the solar wind would cause an outward radial motion
of the Van Allen belts.



Next: Motion in Oscillating Fields
Up: Charged Particle Motion
Previous: Second Adiabatic Invariant
Richard Fitzpatrick
2016-01-23
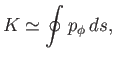
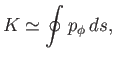
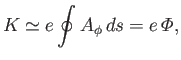
![]() has interesting consequences for charged
particle dynamics in the Earth's inner magnetosphere. Suppose, for instance,
that the
strength of the solar wind were to increase slowly (that is, on timescales
significantly longer than the drift period), thereby, compressing the Earth's
magnetic field. The invariance of
has interesting consequences for charged
particle dynamics in the Earth's inner magnetosphere. Suppose, for instance,
that the
strength of the solar wind were to increase slowly (that is, on timescales
significantly longer than the drift period), thereby, compressing the Earth's
magnetic field. The invariance of
![]() would cause the charged particles
that constitute the Van Allen belts
to move radially inwards, toward the Earth, in order
to conserve the magnetic flux enclosed by their drift orbits. Likewise, a
slow decrease in the strength of the solar wind would cause an outward radial motion
of the Van Allen belts.
would cause the charged particles
that constitute the Van Allen belts
to move radially inwards, toward the Earth, in order
to conserve the magnetic flux enclosed by their drift orbits. Likewise, a
slow decrease in the strength of the solar wind would cause an outward radial motion
of the Van Allen belts.