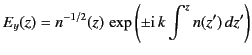 |
(1164) |
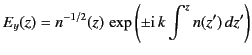 |
(1164) |
It is convenient to define the scaled variable
| (1166) |
We can write
| (1168) |
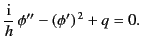 |
(1169) |
Suppose that we keep expanding in powers of ![]() in Equation (1172). The
appropriate generalization of Equation (1173) is a series solution of the
form
in Equation (1172). The
appropriate generalization of Equation (1173) is a series solution of the
form
But, why is it so important that we recognize that WKB solutions are
highly truncated
asymptotic series? The point is that the WKB method was initially
rather controversial
after it was popularized in the 1920s. Many scientists thought that the
method was not mathematically rigorous. Let us try to understand the origin of the problem.
Suppose that we have never heard of an asymptotic series. Looking at
Equation (1174), we would imagine that the expression in square brackets is a power
law expansion in ![]() . The WKB approximation involves neglecting all
terms in this expansion except the first. This sounds fine, as long as
. The WKB approximation involves neglecting all
terms in this expansion except the first. This sounds fine, as long as ![]() is much greater than unity. But, surely, to be mathematically rigorous,
we have to check that the sum of all of the terms in the expansion
that we are neglecting
is small compared to the first term? However, if we attempt this then we discover,
much to our consternation, that the expansion is divergent. In other
words, the sum of all of the neglected terms is infinite! Thus, if
we interpret Equation (1174) as a conventional power law expansion in
is much greater than unity. But, surely, to be mathematically rigorous,
we have to check that the sum of all of the terms in the expansion
that we are neglecting
is small compared to the first term? However, if we attempt this then we discover,
much to our consternation, that the expansion is divergent. In other
words, the sum of all of the neglected terms is infinite! Thus, if
we interpret Equation (1174) as a conventional power law expansion in ![]() then the WKB method is clearly nonsense: in fact, the WKB solution would be the first
approximation to infinity. However, once we appreciate that Equation (1174)
is actually an asymptotic series in
then the WKB method is clearly nonsense: in fact, the WKB solution would be the first
approximation to infinity. However, once we appreciate that Equation (1174)
is actually an asymptotic series in ![]() , the fact that the series diverges becomes
irrelevant. If we retain the first
, the fact that the series diverges becomes
irrelevant. If we retain the first ![]() terms in the series then the series approximates the exact solution of Equation (1169) with an intrinsic (fractional) error which is
of order
terms in the series then the series approximates the exact solution of Equation (1169) with an intrinsic (fractional) error which is
of order ![]() (i.e., the first neglected term in the series). The error is
minimized at a particular value of
(i.e., the first neglected term in the series). The error is
minimized at a particular value of ![]() . As the number of terms in the series is
increased, the intrinsic error decreases, and the value of
. As the number of terms in the series is
increased, the intrinsic error decreases, and the value of ![]() at which the
error is minimized increases. In particular, we can see that there is an
intrinsic error associated with a WKB solution that is of order
at which the
error is minimized increases. In particular, we can see that there is an
intrinsic error associated with a WKB solution that is of order
![]() times the solution.
times the solution.
It is amusing to note that if Equation (1174) were not a divergent series then it
would be impossible to obtain total reflection of the WKB solutions
at the point ![]() . As we shall discover, such reflection is directly
associated with the fact that the expansion (1174) exhibits a Stokes
phenomenon. It is, of course, impossible for a convergent
power series expansion
to exhibit a Stokes phenomenon.
. As we shall discover, such reflection is directly
associated with the fact that the expansion (1174) exhibits a Stokes
phenomenon. It is, of course, impossible for a convergent
power series expansion
to exhibit a Stokes phenomenon.