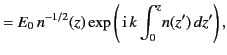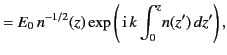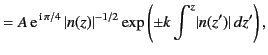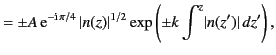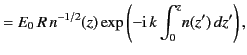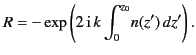Next: Extension to Oblique Incidence
Up: Wave Propagation in Inhomogeneous
Previous: WKB Approximation
Consider an ionosphere in which the refractive index is a slowly varying
function of height  above the surface of
the Earth. Let
above the surface of
the Earth. Let 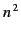 be positive for
be positive for 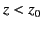 , and negative for
, and negative for
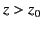 . Suppose that an upgoing radio wave of amplitude
. Suppose that an upgoing radio wave of amplitude 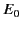 is
generated at ground level (
is
generated at ground level (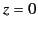 ). The complex amplitude of the wave in the region
). The complex amplitude of the wave in the region
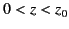 is given by the upgoing WKB solution
is given by the upgoing WKB solution
The upgoing energy flux is given by
 .
In the region
.
In the region 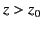 , the WKB solution takes the form
, the WKB solution takes the form
where  is a constant.
These solutions correspond to exponentially growing or decaying waves. Note that
the magnetic components of the waves are in phase quadrature with the
electric components. This implies that the Poynting fluxes of the waves are
zero: in other words„ the waves do not transmit energy. Thus, there is a
non-zero incident energy flux in the region
is a constant.
These solutions correspond to exponentially growing or decaying waves. Note that
the magnetic components of the waves are in phase quadrature with the
electric components. This implies that the Poynting fluxes of the waves are
zero: in other words„ the waves do not transmit energy. Thus, there is a
non-zero incident energy flux in the region 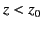 , and zero energy flux in the
region
, and zero energy flux in the
region 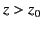 . Clearly, the incident wave is either absorbed or reflected
in the vicinity of the plane
. Clearly, the incident wave is either absorbed or reflected
in the vicinity of the plane 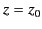 (where
(where 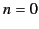 ). In fact, as we shall prove later, the
wave is reflected. The complex amplitude of the reflected wave
in the region
). In fact, as we shall prove later, the
wave is reflected. The complex amplitude of the reflected wave
in the region 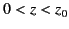 is
given by the downgoing WKB solution
is
given by the downgoing WKB solution
where 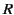 is the coefficient of reflection. Suppose, for the
sake of argument, that the plane
is the coefficient of reflection. Suppose, for the
sake of argument, that the plane 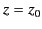 acts like a perfect conductor, so that
acts like a perfect conductor, so that
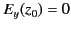 . It follows that
. It follows that
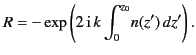 |
(1086) |
In fact, as we shall prove later, the correct answer is
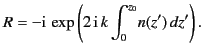 |
(1087) |
Thus, there is only a  phase shift at the reflection point, instead of the
phase shift at the reflection point, instead of the
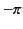 phase shift that would be obtained if the plane
phase shift that would be obtained if the plane 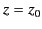 acted like a perfect conductor.
acted like a perfect conductor.



Next: Extension to Oblique Incidence
Up: Wave Propagation in Inhomogeneous
Previous: WKB Approximation
Richard Fitzpatrick
2014-06-27