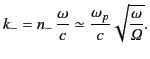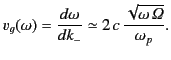Next: Wave Propagation in Dispersive
Up: Wave Propagation in Uniform
Previous: Faraday Rotation
For a plasma (in which
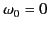 ), the dispersion relation (832) reduces to
), the dispersion relation (832) reduces to
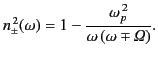 |
(849) |
The upper sign corresponds to a left-hand
circularly polarized wave, and the lower
sign to a right-hand polarized wave. Of course, Equation (850) is only
valid for wave propagation parallel to the direction of the magnetic field.
Wave propagation through the Earth's ionosphere is well described by the
previous dispersion relation. There are wide frequency intervals where
one of 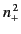 or
or  is positive, and the other negative.
At such frequencies, one state of circular polarization cannot propagate
through the plasma. Consequently, a wave of that polarization incident
on the plasma is totally reflected. (See Chapter 8). The other state of polarization
is partially transmitted.
is positive, and the other negative.
At such frequencies, one state of circular polarization cannot propagate
through the plasma. Consequently, a wave of that polarization incident
on the plasma is totally reflected. (See Chapter 8). The other state of polarization
is partially transmitted.
The behavior of
 at low frequencies is responsible for
a strange phenomenon known to radio hams as ``whistlers.''
As the wave frequency tends to zero, Equation (850) yields
at low frequencies is responsible for
a strange phenomenon known to radio hams as ``whistlers.''
As the wave frequency tends to zero, Equation (850) yields
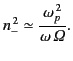 |
(850) |
At such a frequency, 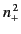 is negative, so only right-hand
polarized waves can propagate. The wavenumber of these waves is given by
is negative, so only right-hand
polarized waves can propagate. The wavenumber of these waves is given by
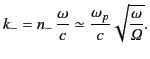 |
(851) |
Now, energy propagates through a dispersive medium at the group velocity
(see Section 7.13)
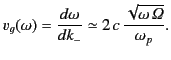 |
(852) |
Thus, low frequency waves transmit energy at a slower rate than high frequency
waves. A lightning strike in one hemisphere of the Earth generates a
wide spectrum of radiation, some of which propagates along the dipolar
field-lines of the Earth's magnetic field in a manner described approximately
by the dispersion relation (851). The high frequency components of the signal
return to the surface of the Earth before the low frequency components
(because they travel faster along the magnetic field). This gives rise
to a radio signal that begins at a high frequency, and then
``whistles'' down
to lower frequencies.



Next: Wave Propagation in Dispersive
Up: Wave Propagation in Uniform
Previous: Faraday Rotation
Richard Fitzpatrick
2014-06-27
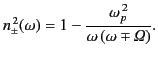
![]() at low frequencies is responsible for
a strange phenomenon known to radio hams as ``whistlers.''
As the wave frequency tends to zero, Equation (850) yields
at low frequencies is responsible for
a strange phenomenon known to radio hams as ``whistlers.''
As the wave frequency tends to zero, Equation (850) yields