


Next: Permanent Ferromagnets
Up: Magnetostatics in Magnetic Media
Previous: Ferromagnetism
Let us derive the matching conditions for 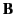 and
and  at
the boundary between two magnetic media. The governing equations for a steady-state situation are
at
the boundary between two magnetic media. The governing equations for a steady-state situation are
 |
(694) |
and
 |
(695) |
Integrating Equation (695) over a Gaussian pill-box enclosing part of the
boundary surface between the two media gives
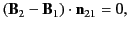 |
(696) |
where
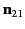 is the unit
normal to this surface directed from
medium 1 to medium 2. Integrating Equation (696) around a small loop that
straddles the boundary surface yields
is the unit
normal to this surface directed from
medium 1 to medium 2. Integrating Equation (696) around a small loop that
straddles the boundary surface yields
 |
(697) |
assuming that there is no true current sheet flowing at the surface.
In general, there is a magnetization current sheet flowing
at the boundary surface whose density is given by
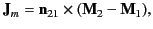 |
(698) |
where 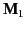 is the magnetization in medium 1 at the boundary,
et cetera. It is clear that the normal component of the magnetic field,
and the tangential component of the magnetic intensity, are both
continuous across any boundary between magnetic materials.
is the magnetization in medium 1 at the boundary,
et cetera. It is clear that the normal component of the magnetic field,
and the tangential component of the magnetic intensity, are both
continuous across any boundary between magnetic materials.



Next: Permanent Ferromagnets
Up: Magnetostatics in Magnetic Media
Previous: Ferromagnetism
Richard Fitzpatrick
2014-06-27