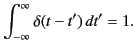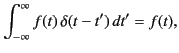Next: Three-Dimensional Dirac Delta Function
Up: Maxwell's Equations
Previous: Scalar and Vector Potentials
The Dirac delta function,
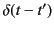 , has the property
, has the property
In addition, however, the function is singular at 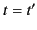 in such a manner
that
in such a manner
that
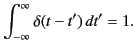 |
(18) |
It follows that
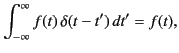 |
(19) |
where 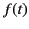 is an arbitrary function that is well behaved at
is an arbitrary function that is well behaved at 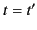 . It is also easy to see that
. It is also easy to see that
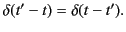 |
(20) |
Richard Fitzpatrick
2014-06-27