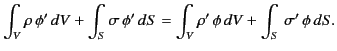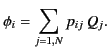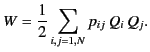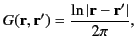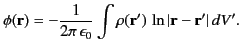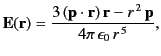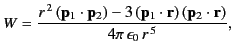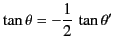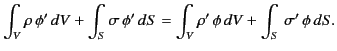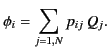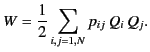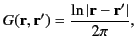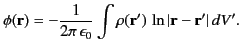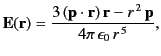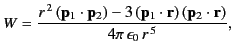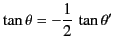Next: Potential Theory
Up: Electrostatic Fields
Previous: Dirichlet Green's Function for
- Prove the mean value theorem: for charge-free space the value of the electrostatic potential at any point is
equal to the average of the potential over the surface of any sphere centered on that point.
- Prove Green's reciprocation theorem: if
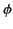 is the potential due to a volume
charge density
is the potential due to a volume
charge density 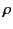 within a volume
within a volume 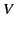 and a surface charge density
and a surface charge density 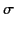 on the conducting surface
on the conducting surface 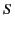 bounding the
volume
bounding the
volume 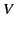 , while
, while 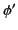 is the potential due to another charge distribution
is the potential due to another charge distribution 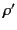 and
and 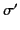 (non-simultaneously occupying the same volume and the same
surface, respectively), then
(non-simultaneously occupying the same volume and the same
surface, respectively), then
- Two infinite grounded parallel conducting planes are separated by a distance
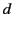 . A point charge
. A point charge 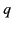 is
placed between the planes. Use Green's reciprocation theorem to prove that the total charge induced on
one of the planes is equal to
is
placed between the planes. Use Green's reciprocation theorem to prove that the total charge induced on
one of the planes is equal to 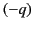 times the fractional perpendicular distance of the point charge from the
other plane. [Hint: Choose as your comparison electrostatic problem with the same surfaces one whose charge
densities and potential are known and simple.]
times the fractional perpendicular distance of the point charge from the
other plane. [Hint: Choose as your comparison electrostatic problem with the same surfaces one whose charge
densities and potential are known and simple.]
- Consider two insulated conductors, labeled 1 and 2. Let
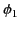 be the
potential of the first conductor when it is uncharged and the second conductor holds a
charge
be the
potential of the first conductor when it is uncharged and the second conductor holds a
charge 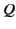 . Likewise, let
. Likewise, let 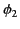 be the potential of the second conductor
when it is uncharged and the first conductor holds a charge
be the potential of the second conductor
when it is uncharged and the first conductor holds a charge 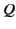 . Use Green's
reciprocation theorem to demonstrate that
. Use Green's
reciprocation theorem to demonstrate that
- Consider two insulated spherical conductors. Let the
first have radius
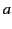 . Let the second be sufficiently small that it
can effectively be treated as a point charge, and let it also be located a distance
. Let the second be sufficiently small that it
can effectively be treated as a point charge, and let it also be located a distance 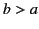 from
the center of the first. Suppose that the first conductor is uncharged, and that the second carries a charge
from
the center of the first. Suppose that the first conductor is uncharged, and that the second carries a charge 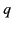 . What is the potential of the first conductor?
[Hint: Consider the result proved in Exercise 1.]
. What is the potential of the first conductor?
[Hint: Consider the result proved in Exercise 1.]
- Consider a set of
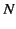 conductors distributed in a vacuum. Suppose that
the
conductors distributed in a vacuum. Suppose that
the 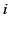 th conductor carries the charge
th conductor carries the charge 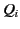 and is at the scalar potential
and is at the scalar potential
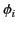 . It follows from the linearity of Maxwell's equations and Ohm's law
that a linear relationship exists between the potentials and the charges:
that is,
. It follows from the linearity of Maxwell's equations and Ohm's law
that a linear relationship exists between the potentials and the charges:
that is,
Here, the 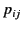 are termed the coefficients of potential. Demonstrate that
are termed the coefficients of potential. Demonstrate that
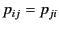 for all
for all 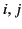 . [Hint: Consider the result
proved in Exercise 1.] Show that the total electrostatic potential energy of
the charged conductors is
. [Hint: Consider the result
proved in Exercise 1.] Show that the total electrostatic potential energy of
the charged conductors is
- Demonstrate that the Green's function for Poisson's equation in two
dimensions (i.e.,
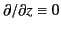 ) is
) is
where
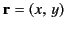 , et cetera.
Hence, deduce that the scalar potential field generated by the two-dimensional
charge distribution
, et cetera.
Hence, deduce that the scalar potential field generated by the two-dimensional
charge distribution
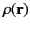 is
is
- A electric dipole of fixed moment
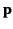 is situated at position
is situated at position
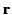 in a non-uniform external electric field
in a non-uniform external electric field
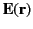 . Demonstrate
that the net force on the dipole can be written
. Demonstrate
that the net force on the dipole can be written
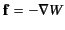 , where
, where
- Demonstrate that the electric field generated by an electric dipole of dipole moment
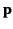 is
is
where 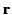 represents vector displacement relative to the dipole.
Show that the potential energy of an electric dipole of moment
represents vector displacement relative to the dipole.
Show that the potential energy of an electric dipole of moment 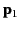 in the electric field generated by a second dipole of moment
in the electric field generated by a second dipole of moment 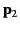 is
is
where 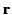 is the displacement of one dipole from another.
is the displacement of one dipole from another.
- Show that the torque on an electric dipole of moment
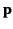 in a uniform
external electric field
in a uniform
external electric field 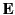 is
is
Hence, deduce that the potential energy of the dipole is
- Consider two coplanar electric dipoles with their centers a fixed distance apart. Show that if the angles the dipoles
make with the line joining their centers are
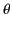 and
and 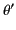 , respectively, and
, respectively, and 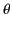 is held fixed, then
is held fixed, then
in equilibrium.



Next: Potential Theory
Up: Electrostatic Fields
Previous: Dirichlet Green's Function for
Richard Fitzpatrick
2014-06-27