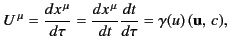Next: Current Density 4-Vector
Up: Relativity and Electromagnetism
Previous: Proper Time
We have seen that the quantity
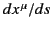 transforms as a 4-vector under
a general Lorentz transformation [see Equation (1686)]. Because
transforms as a 4-vector under
a general Lorentz transformation [see Equation (1686)]. Because
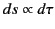 it follows that
it follows that
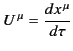 |
(1721) |
also transforms as a 4-vector. This quantity is known as the 4-velocity.
Likewise, the quantity
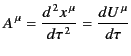 |
(1722) |
is a 4-vector, and is called the 4-acceleration.
For events along the world-line of a particle traveling with 3-velocity
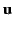 , we have
, we have
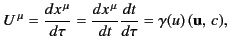 |
(1723) |
where use has been made of Equation (1719). This gives the relationship between
a particle's 3-velocity and its 4-velocity. The relationship between the
3-acceleration and the 4-acceleration is less straightforward. We
have
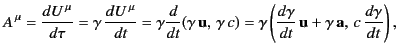 |
(1724) |
where
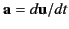 is the 3-acceleration.
In the rest frame of the particle,
is the 3-acceleration.
In the rest frame of the particle,
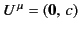 and
and
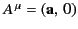 . It follows that
. It follows that
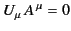 |
(1725) |
(note that
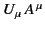 is an invariant quantity).
In other words, the 4-acceleration of a particle is always orthogonal
to its 4-velocity.
is an invariant quantity).
In other words, the 4-acceleration of a particle is always orthogonal
to its 4-velocity.



Next: Current Density 4-Vector
Up: Relativity and Electromagnetism
Previous: Proper Time
Richard Fitzpatrick
2014-06-27
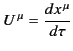
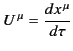
![]() , we have
, we have