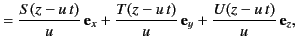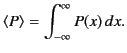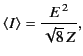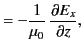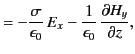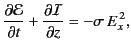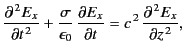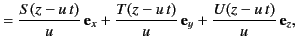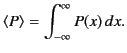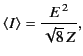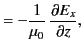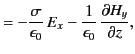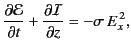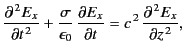Next: Wave Propagation in Inhomogeneous
Up: Wave Propagation in Uniform
Previous: Signal Arrival
- A general electromagnetic wave pulse propagating in the
 -direction at velocity
-direction at velocity  is written
is written
where 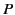 ,
, 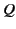 ,
, 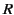 ,
, 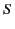 ,
, 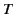 , and
, and 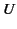 are arbitrary functions. In order
to exclude electrostatic and magnetostatic fields, these functions are subject to
the constraint that
are arbitrary functions. In order
to exclude electrostatic and magnetostatic fields, these functions are subject to
the constraint that
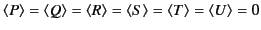 , where
, where
Suppose that the pulse propagates through a uniform dielectric medium of
dielectric constant 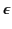 . Demonstrate from Maxwell's equation that
. Demonstrate from Maxwell's equation that
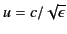 ,
, 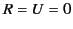 ,
, 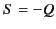 , and
, and 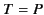 . Incidentally, this result implies that a general
wave pulse is characterized by two arbitrary functions, corresponding
to the two possible independent polarizations of the pulse.
. Incidentally, this result implies that a general
wave pulse is characterized by two arbitrary functions, corresponding
to the two possible independent polarizations of the pulse.
- Show that the mean energy flux due to an electromagnetic wave of angular frequency
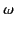 propagating though a good
conductor of conductivity
propagating though a good
conductor of conductivity 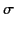 can be written
can be written
where 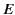 is the peak electric field-strength, and
is the peak electric field-strength, and
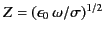 .
.
- Consider an electromagnetic wave propagating in the positive
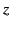 -direction through a good
conductor of conductivity
-direction through a good
conductor of conductivity 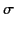 . Suppose that the wave electric field is
. Suppose that the wave electric field is
where 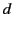 is the skin-depth. Demonstrate that the mean electromagnetic energy flux across the plane
is the skin-depth. Demonstrate that the mean electromagnetic energy flux across the plane 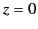 matches the
mean rate at which electromagnetic energy is dissipated per unit area due to Joule heating in the region
matches the
mean rate at which electromagnetic energy is dissipated per unit area due to Joule heating in the region 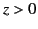 .
.
- A plane electromagnetic wave, linearly polarized in the
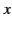 -direction, and propagating in the
-direction, and propagating in the 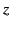 -direction through an electrical
conducting medium of conductivity
-direction through an electrical
conducting medium of conductivity 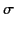 and relative dielectric constant unity, is governed by
and relative dielectric constant unity, is governed by
where 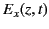 and
and 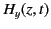 are the electric and magnetic components
of the wave.
Derive an energy conservation equation of the form
are the electric and magnetic components
of the wave.
Derive an energy conservation equation of the form
where 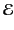 is the electromagnetic energy per unit volume, and
is the electromagnetic energy per unit volume, and 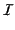 the electromagnetic energy flux.
Give expressions for
the electromagnetic energy flux.
Give expressions for 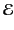 and
and 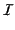 . What does the right-hand side of the
previous equation represent? Demonstrate that
. What does the right-hand side of the
previous equation represent? Demonstrate that 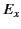 obeys the wave-diffusion
equation
obeys the wave-diffusion
equation
where
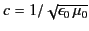 . Consider the high frequency, low conductivity, limit
. Consider the high frequency, low conductivity, limit
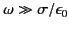 . Show that a wave propagating into the medium varies as
. Show that a wave propagating into the medium varies as
where
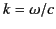 ,
,
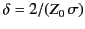 , and
, and
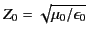 .
Demonstrate that
.
Demonstrate that
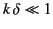 : that is, the wave penetrates many wavelengths into the medium.
: that is, the wave penetrates many wavelengths into the medium.
- Consider a uniform plasma of plasma frequency
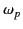 containing a uniform magnetic field
containing a uniform magnetic field
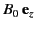 . Show that left-hand
circularly polarized electromagnetic waves can only propagate parallel to the
magnetic field provided that
. Show that left-hand
circularly polarized electromagnetic waves can only propagate parallel to the
magnetic field provided that
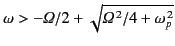 , where
, where
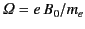 is the electron cyclotron frequency.
Demonstrate that right-hand circularly polarized electromagnetic waves can only propagate
parallel to the magnetic field provided that their frequencies do
not lie in the range
is the electron cyclotron frequency.
Demonstrate that right-hand circularly polarized electromagnetic waves can only propagate
parallel to the magnetic field provided that their frequencies do
not lie in the range
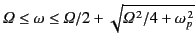 .
.



Next: Wave Propagation in Inhomogeneous
Up: Wave Propagation in Uniform
Previous: Signal Arrival
Richard Fitzpatrick
2014-06-27