


Next: Clausius-Mossotti Relation
Up: Electrostatics in Dielectric Media
Previous: Energy Density Within Dielectric
Equation (567) was derived by considering a virtual process in which
true charges are added to a system of charges and dielectrics that are
held fixed, so that no mechanical work is done against physical
displacements. Consider a different virtual process in which
the physical coordinates of the charges and dielectric are given a virtual
displacement
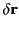 at each point in space, but no free charges
are added to the system. Because we are dealing with a conservative system,
the energy expression (567) can still be employed, despite the fact that
it was derived in terms of another virtual process. The variation in
the total electrostatic energy
at each point in space, but no free charges
are added to the system. Because we are dealing with a conservative system,
the energy expression (567) can still be employed, despite the fact that
it was derived in terms of another virtual process. The variation in
the total electrostatic energy  when the system undergoes a virtual
displacement
when the system undergoes a virtual
displacement
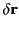 is related to the electrostatic
force density,
is related to the electrostatic
force density, 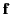 ,
acting within the dielectric medium via
,
acting within the dielectric medium via
 |
(568) |
If the medium is moving with a velocity field 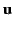 then
the rate at which electrostatic energy is drained from the
then
the rate at which electrostatic energy is drained from the
 and
and 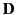 fields is given
by
fields is given
by
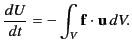 |
(569) |
Consider the energy increment due to a change,
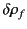 ,
in the free charge distribution, and a change,
,
in the free charge distribution, and a change,
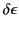 , in the
dielectric constant, which are both assumed to be caused by the virtual displacement. From Equation (567),
, in the
dielectric constant, which are both assumed to be caused by the virtual displacement. From Equation (567),
![$\displaystyle \delta U = \frac{1}{2\,\epsilon_0}\int_V \left[D^{\,2}\,\delta(1/\epsilon) + 2 \,{\bf D} \cdot \delta {\bf D}/\epsilon\right]dV,$](img1211.png) |
(570) |
or
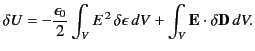 |
(571) |
Here, the first term represents the energy increment due to the change
in dielectric constant associated with the virtual displacement, whereas
the second term corresponds to the energy increment caused by displacement
of the free charges. The second term can be written
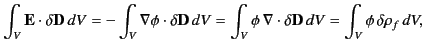 |
(572) |
where surface terms have been neglected. Thus, Equation (572) implies
that
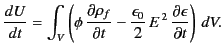 |
(573) |
In order to arrive at an expression for the force density, 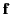 , we
need to express the time derivatives
, we
need to express the time derivatives
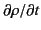 and
and
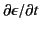 in terms of the velocity field,
in terms of the velocity field, 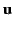 .
This can be achieved by adopting a dielectric equation of state:
that is, a relation that specifies the dependence of the dielectric
constant,
.
This can be achieved by adopting a dielectric equation of state:
that is, a relation that specifies the dependence of the dielectric
constant,  , on the mass density,
, on the mass density, 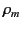 . Let us assume that
. Let us assume that
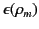 is a known function. It follows that
is a known function. It follows that
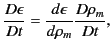 |
(574) |
where
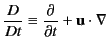 |
(575) |
is the total time derivative (i.e., the time
derivative in a frame of reference that
is locally co-moving with the dielectric.)
The hydrodynamic equation of continuity of the dielectric is
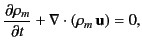 |
(576) |
which implies that
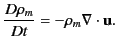 |
(577) |
It follows that
 |
(578) |
The conservation equation for the free charges is written
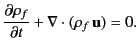 |
(579) |
Thus, we can express Equation (574) in the form
![$\displaystyle \frac{dU}{dt} = \int_V\left[-\phi\,\nabla \cdot(\rho_f\,{\bf u}) ...
...u} + \frac{\epsilon_0}{2} \,E^{\,2}\,\nabla\epsilon\, \cdot {\bf u}\right]\,dV.$](img1225.png) |
(580) |
Integrating the first term by parts, and neglecting any surface contributions,
we obtain
 |
(581) |
Likewise,
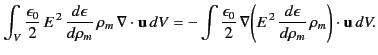 |
(582) |
Thus, Equation (581) becomes
![$\displaystyle \frac{dU}{dt} = \int_V\left[-\rho_f \,{\bf E} +\frac{\epsilon_0}{...
...ft(E^{\,2}\,\frac{d\epsilon}{d\rho_m}\,\rho_m\right) \right]\cdot {\bf u}\, dV.$](img1228.png) |
(583) |
Comparing with Equation (570), we deduce that the force density inside the
dielectric is
given by
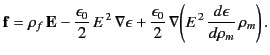 |
(584) |
The first term in the above equation is the standard electrostatic
force density (due to the presence of free charges). The second term represents a force that appears whenever
an inhomogeneous dielectric is placed in an electric field. The last
term, which is known as the electrostriction term, gives a force acting
on a dielectric in an inhomogeneous electric field. Note that the
magnitude of the electrostriction force density depends explicitly on the
dielectric equation of state of the material, through
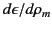 .
The electrostriction term gives zero net force acting on any finite region
of dielectric, provided we can integrate over a large enough portion of the dielectric that its extremities lie in a field-free region. For this reason,
the term is frequently omitted, because in the calculation of the
total forces acting on dielectric bodies it usually makes no contribution.
Note, however, that if the electrostriction
term is omitted then an incorrect pressure
variation within the dielectric is obtained, even though the total force is
given correctly.
.
The electrostriction term gives zero net force acting on any finite region
of dielectric, provided we can integrate over a large enough portion of the dielectric that its extremities lie in a field-free region. For this reason,
the term is frequently omitted, because in the calculation of the
total forces acting on dielectric bodies it usually makes no contribution.
Note, however, that if the electrostriction
term is omitted then an incorrect pressure
variation within the dielectric is obtained, even though the total force is
given correctly.



Next: Clausius-Mossotti Relation
Up: Electrostatics in Dielectric Media
Previous: Energy Density Within Dielectric
Richard Fitzpatrick
2014-06-27


![]() ,
in the free charge distribution, and a change,
,
in the free charge distribution, and a change,
![]() , in the
dielectric constant, which are both assumed to be caused by the virtual displacement. From Equation (567),
, in the
dielectric constant, which are both assumed to be caused by the virtual displacement. From Equation (567),
![$\displaystyle \delta U = \frac{1}{2\,\epsilon_0}\int_V \left[D^{\,2}\,\delta(1/\epsilon) + 2 \,{\bf D} \cdot \delta {\bf D}/\epsilon\right]dV,$](img1211.png)
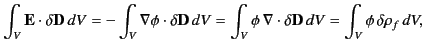
![]() , we
need to express the time derivatives
, we
need to express the time derivatives
![]() and
and
![]() in terms of the velocity field,
in terms of the velocity field, ![]() .
This can be achieved by adopting a dielectric equation of state:
that is, a relation that specifies the dependence of the dielectric
constant,
.
This can be achieved by adopting a dielectric equation of state:
that is, a relation that specifies the dependence of the dielectric
constant, ![]() , on the mass density,
, on the mass density, ![]() . Let us assume that
. Let us assume that
![]() is a known function. It follows that
is a known function. It follows that
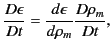
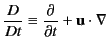
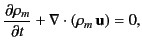
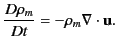

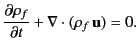

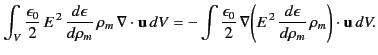
![$\displaystyle \frac{dU}{dt} = \int_V\left[-\rho_f \,{\bf E} +\frac{\epsilon_0}{...
...ft(E^{\,2}\,\frac{d\epsilon}{d\rho_m}\,\rho_m\right) \right]\cdot {\bf u}\, dV.$](img1228.png)
![]() .
The electrostriction term gives zero net force acting on any finite region
of dielectric, provided we can integrate over a large enough portion of the dielectric that its extremities lie in a field-free region. For this reason,
the term is frequently omitted, because in the calculation of the
total forces acting on dielectric bodies it usually makes no contribution.
Note, however, that if the electrostriction
term is omitted then an incorrect pressure
variation within the dielectric is obtained, even though the total force is
given correctly.
.
The electrostriction term gives zero net force acting on any finite region
of dielectric, provided we can integrate over a large enough portion of the dielectric that its extremities lie in a field-free region. For this reason,
the term is frequently omitted, because in the calculation of the
total forces acting on dielectric bodies it usually makes no contribution.
Note, however, that if the electrostriction
term is omitted then an incorrect pressure
variation within the dielectric is obtained, even though the total force is
given correctly.