


Next: Boundary Conditions for and
Up: Electrostatics in Dielectric Media
Previous: Electrostatics in Dielectric Media
The terrestrial environment is characterized by
dielectric media (e.g.,
air and water) that are, for the most part, electrically neutral, because they
are made up of neutral atoms and molecules. However, when the constituent
atoms and
molecules of such media are placed in an electric field they tend to polarize: that is, to develop electric dipole moments.
Suppose that when a given neutral molecule is placed in an electric
field,  , the centre of charge of its
constituent electrons (whose total
charge is
, the centre of charge of its
constituent electrons (whose total
charge is 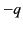 ) is displaced by a distance
) is displaced by a distance  with respect
to the centre of charge of its nucleus (whose charge is
with respect
to the centre of charge of its nucleus (whose charge is 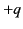 ). The dipole moment
of the molecule is then
). The dipole moment
of the molecule is then
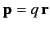 . (See Section 2.7.) If there are
. (See Section 2.7.) If there are
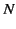 such molecules per unit volume then the electric polarization
such molecules per unit volume then the electric polarization
 (i.e., the dipole moment per unit volume) is
given by
(i.e., the dipole moment per unit volume) is
given by
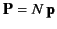 . More generally,
. More generally,
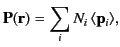 |
(496) |
where
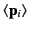 is the
average dipole moment of the
is the
average dipole moment of the 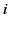 th type of molecule
in the vicinity of point
th type of molecule
in the vicinity of point  ,
and
,
and 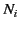 is the average number of such molecules per unit volume at
is the average number of such molecules per unit volume at  .
.
It is easily demonstrated [e.g., by integrating Equation (201) by parts, and then comparing the result with Equation (162)] that any divergence of the polarization
field,
 , gives rise to a charge density,
, gives rise to a charge density,
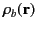 ,
in the medium. In fact,
,
in the medium. In fact,
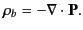 |
(497) |
This density is attributable to bound charges (i.e.,
charges that arise from the polarization of neutral atoms), and
is usually distinguished from the charge density, 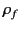 , due to
free charges, which represents a net surplus or
deficit of electrons in the medium. Thus, the total
charge density,
, due to
free charges, which represents a net surplus or
deficit of electrons in the medium. Thus, the total
charge density, 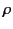 , in the medium is
, in the medium is
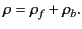 |
(498) |
It must be emphasized that both terms on the right-hand side of this equation represent real
physical charge. Nevertheless, it is useful to make the distinction
between bound and free charges, especially when it comes to working out
the energy associated with electric fields in dielectric media.
Gauss' law takes the differential form
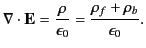 |
(499) |
This expression can be rearranged to give
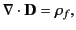 |
(500) |
where
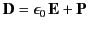 |
(501) |
is termed the electric displacement (which should not be confused with dipole moment per unit area--see Section 2.8), and has the same dimensions
as  (i.e., dipole moment
per unit volume). The divergence theorem tells us that
(i.e., dipole moment
per unit volume). The divergence theorem tells us that
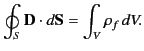 |
(502) |
In other words, the flux of 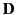 out of some closed surface
out of some closed surface  is equal to the total free charge enclosed within that surface. Unlike the
electric field
is equal to the total free charge enclosed within that surface. Unlike the
electric field  (which is the force acting on unit charge),
or the polarization
(which is the force acting on unit charge),
or the polarization  (which is the dipole moment per unit volume),
the electric displacement
(which is the dipole moment per unit volume),
the electric displacement 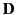 has no clear physical meaning.
The only reason for introducing this quantity is that it enables us to
calculate electric fields in the presence of dielectric materials without first
having to know the distribution of bound charges. However,
this is only possible if we have a constitutive
relation connecting
has no clear physical meaning.
The only reason for introducing this quantity is that it enables us to
calculate electric fields in the presence of dielectric materials without first
having to know the distribution of bound charges. However,
this is only possible if we have a constitutive
relation connecting  and
and 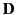 . It is conventional
to assume that the induced polarization,
. It is conventional
to assume that the induced polarization,  , is
directly proportional to the electric field,
, is
directly proportional to the electric field,  , so that
, so that
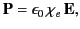 |
(503) |
where 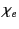 is termed the medium's electric susceptibility.
It follows that
is termed the medium's electric susceptibility.
It follows that
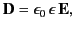 |
(504) |
where the dimensionless quantity
 |
(505) |
is known as the relative dielectric constant or relative permittivity of the medium.
It follows from Equations (501) and (505)
that
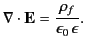 |
(506) |
Thus, the electric fields produced by free charges in a dielectric medium are analogous
to those produced by the same charges in a vacuum, except that they are reduced by
a factor  . This reduction can be understood in terms of a
polarization of the medium's constituent atoms or molecules that produces
electric fields in opposition to those of the free charges. One immediate
consequence is that the capacitance of a capacitor is increased by a factor
. This reduction can be understood in terms of a
polarization of the medium's constituent atoms or molecules that produces
electric fields in opposition to those of the free charges. One immediate
consequence is that the capacitance of a capacitor is increased by a factor
 if the empty space between the electrodes is filled with a
dielectric medium of dielectric constant
if the empty space between the electrodes is filled with a
dielectric medium of dielectric constant  (assuming that
fringing fields can be neglected).
(assuming that
fringing fields can be neglected).
It must be understood that Equations (504)-(507) constitute an approximation
that is generally found to hold under terrestrial conditions (provided
the electric field-strength does not become too large) when dealing with isotropic media. For anisotropic
media (e.g., crystals), Equation (505) generalizes to
where
 is a symmetric second-rank tensor known as the
dielectric tensor. For strong electric fields,
is a symmetric second-rank tensor known as the
dielectric tensor. For strong electric fields,
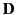 ceases to vary linearly with
ceases to vary linearly with  . Indeed, for sufficiently
strong electric fields, neutral molecules are disrupted, and the medium becomes a plasma.
. Indeed, for sufficiently
strong electric fields, neutral molecules are disrupted, and the medium becomes a plasma.



Next: Boundary Conditions for and
Up: Electrostatics in Dielectric Media
Previous: Electrostatics in Dielectric Media
Richard Fitzpatrick
2014-06-27
![]() , gives rise to a charge density,
, gives rise to a charge density,
![]() ,
in the medium. In fact,
,
in the medium. In fact,