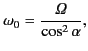Next: About this document ...
Up: Relativity and Electromagnetism
Previous: Synchrotron Radiation
- Consider two Cartesian reference frames,
 and
and  , in the
standard configuration. Suppose that
, in the
standard configuration. Suppose that  moves with constant
velocity
moves with constant
velocity  with respect to
with respect to  along their common
along their common  -axis.
Demonstrate that the Lorentz transformation between coordinates in the
two frames can be written
-axis.
Demonstrate that the Lorentz transformation between coordinates in the
two frames can be written
where
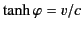 .
Show that the previous transformation is equivalent to a rotation through
an angle
.
Show that the previous transformation is equivalent to a rotation through
an angle
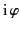 , in the
, in the  -
-
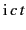 plane, in
(
plane, in
( ,
, 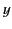 ,
,  ,
,
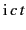 ) space.
) space.
- Show that, in the standard configuration, two successive Lorentz transformations with velocities
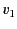 and
and 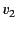 are equivalent to
a single Lorentz transformation with velocity
are equivalent to
a single Lorentz transformation with velocity
- Let
 and
and  be the displacement vectors of some particle in the Cartesian reference frames
be the displacement vectors of some particle in the Cartesian reference frames  and
and  , respectively. Suppose that frame
, respectively. Suppose that frame  moves with
velocity
moves with
velocity  with respect to frame
with respect to frame  . Demonstrate that a
general Lorentz transformation takes the form
. Demonstrate that a
general Lorentz transformation takes the form
where
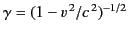 . If
. If
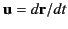 and
and
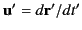 are the particle's velocities in the two
reference frames, respectively, demonstrate that a general velocity transformation
is written
are the particle's velocities in the two
reference frames, respectively, demonstrate that a general velocity transformation
is written
- Let
 be the Earth's approximately constant orbital speed.
Demonstrate that the direction of starlight incident at right-angles to the Earth's
instantaneous direction of motion appears slightly shifted in the Earth's
instantaneous rest frame by an angle
be the Earth's approximately constant orbital speed.
Demonstrate that the direction of starlight incident at right-angles to the Earth's
instantaneous direction of motion appears slightly shifted in the Earth's
instantaneous rest frame by an angle
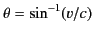 . This
effect is known as the abberation of starlight. Estimate the
magnitude of
. This
effect is known as the abberation of starlight. Estimate the
magnitude of  (in arc seconds).
(in arc seconds).
- Let
 and
and  be the electric and magnetic field, respectively,
in some Cartesian reference frame
be the electric and magnetic field, respectively,
in some Cartesian reference frame  . Likewise, let
. Likewise, let 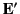 and
and 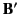 be the electric and magnetic field, respectively, in some other Cartesian
frame
be the electric and magnetic field, respectively, in some other Cartesian
frame  , which moves with velocity
, which moves with velocity  with respect to
with respect to  .
Demonstrate that the general transformation of fields takes the form
.
Demonstrate that the general transformation of fields takes the form
where
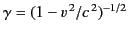 .
.
- A particle of rest mass
 and charge
and charge 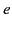 moves relativistically
in a uniform magnetic field of strength
moves relativistically
in a uniform magnetic field of strength 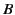 . Show that the particle's
trajectory is a helix aligned along the direction of the field, and that
the particle drifts parallel to the field at a uniform
velocity, and gyrates in the plane perpendicular to the field with constant
angular velocity
. Show that the particle's
trajectory is a helix aligned along the direction of the field, and that
the particle drifts parallel to the field at a uniform
velocity, and gyrates in the plane perpendicular to the field with constant
angular velocity
Here,
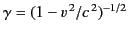 , and
, and  is the particle's (constant)
speed.
is the particle's (constant)
speed.
- Let
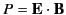 and
and
 . Prove the
following statements, assuming that
. Prove the
following statements, assuming that 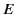 and
and 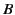 are not both zero.
are not both zero.
- At any given event,
 is perpendicular to
is perpendicular to  either in all
frames of reference, or in none. Moreover, each of the three relations
either in all
frames of reference, or in none. Moreover, each of the three relations
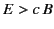 ,
, 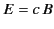 , and
, and 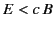 holds in all frames or in none.
holds in all frames or in none.
- If
 then the field is said to be null. For a null field,
then the field is said to be null. For a null field,
 is perpendicular to
is perpendicular to  , and
, and 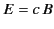 , in all frames.
, in all frames.
- If
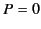 and
and 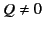 then there are infinitely many frames (with
a common relative direction of motion) in which
then there are infinitely many frames (with
a common relative direction of motion) in which 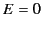 or
or 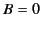 , according
as
, according
as 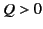 or
or 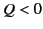 , and none other. Precisely one of these frames
moves in the direction
, and none other. Precisely one of these frames
moves in the direction
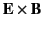 , its velocity being
, its velocity being
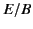 or
or
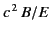 , respectively.
, respectively.
- If
 then there are infinitely many frames (with a common
direction of motion) in which
then there are infinitely many frames (with a common
direction of motion) in which  is parallel to
is parallel to  , and
none other. Precisely one of these moves in the direction
, and
none other. Precisely one of these moves in the direction
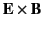 , its velocity being given by the smaller root of the quadratic
equation
, its velocity being given by the smaller root of the quadratic
equation
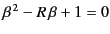 , where
, where 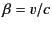 , and
, and
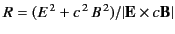 . In order for
. In order for  to be real
we require
to be real
we require 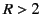 . Demonstrate that this is always the case.
. Demonstrate that this is always the case.
- In the rest frame of a conducting medium, the current density satisfies
Ohm's law
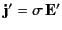 , where
, where 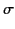 is the conductivity,
and primes denote quantities in the rest frame.
is the conductivity,
and primes denote quantities in the rest frame.
- Taking into account the possibility of convection currents, as
well as conduction currents, show that the covariant generalization
of Ohm's law is
where  is the 4-velocity of the medium,
is the 4-velocity of the medium, 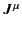 the
4-current, and
the
4-current, and
 the electromagnetic field tensor.
the electromagnetic field tensor.
- Show that if the medium has a velocity

 with
respect to some inertial frame then the 3-vector current in that frame
is
with
respect to some inertial frame then the 3-vector current in that frame
is
where 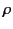 is the charge density observed in the inertial frame.
is the charge density observed in the inertial frame.
- Consider the relativistically covariant form of Maxwell's equations
in the presence of magnetic monopoles. Demonstrate that it
is possible to define a proper-4-current
and a pseudo-4-current
where  and
and 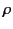 are the flux and density of electric
charges, respectively, whereas
are the flux and density of electric
charges, respectively, whereas 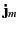 and
and 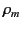 are
the flux and density of magnetic monopoles, respectively. Show that
the conservation laws for electric charges and magnetic monopoles take the
form
are
the flux and density of magnetic monopoles, respectively. Show that
the conservation laws for electric charges and magnetic monopoles take the
form
respectively.
Finally, if
 is the electromagnetic field tensor, and
is the electromagnetic field tensor, and
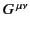 its dual, show that Maxwell's equations are equivalent to
its dual, show that Maxwell's equations are equivalent to
- Prove that the electromagnetic energy tensor satisfies the following
two identities:
and
where
- A charge
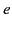 moves in simple harmonic motion along the
moves in simple harmonic motion along the  axis,
such that its retarded position is
axis,
such that its retarded position is
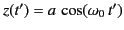 .
.
- Show that the instantaneous power radiated per unit solid angle is
where
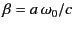 , and
, and  is a standard spherical polar
coordinate.
is a standard spherical polar
coordinate.
- By time averaging, show that the average power radiated per unit solid angle is
- Sketch the angular distribution of the radiation for non-relativistic
and ultra-relativistic motion.
- The trajectory of a relativistic particle of charge
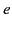 and rest mass
and rest mass  in a uniform magnetic field
in a uniform magnetic field  is a helix aligned with the field. Let the pitch angle of the
helix be
is a helix aligned with the field. Let the pitch angle of the
helix be 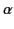 (so,
(so, 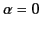 corresponds to circular motion).
By arguments similar to those used for synchrotron radiation, show
that an observer far from the charge would detect radiation with a
fundamental frequency
corresponds to circular motion).
By arguments similar to those used for synchrotron radiation, show
that an observer far from the charge would detect radiation with a
fundamental frequency
where
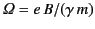 , and that the spectrum would extend up to
frequencies of order
, and that the spectrum would extend up to
frequencies of order



Next: About this document ...
Up: Relativity and Electromagnetism
Previous: Synchrotron Radiation
Richard Fitzpatrick
2014-06-27
![$\displaystyle = {\bf r} + \left[\frac{(\gamma-1)\,{\bf r}\cdot{\bf v}}{v^{\,2}} - \gamma\,t\right]{\bf v},$](img4169.png)
![$\displaystyle {\bf u}' = \frac{{\bf u}+ \left[(\gamma-1)\,{\bf u}\cdot{\bf v}/c^{\,2} - \gamma\right]{\bf v}}{\gamma\,(1-{\bf u}\cdot{\bf v}/c^{\,2})}.
$](img4174.png)
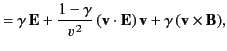

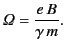
 is perpendicular to
is perpendicular to  either in all
frames of reference, or in none. Moreover, each of the three relations
either in all
frames of reference, or in none. Moreover, each of the three relations
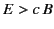 ,
, 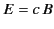 , and
, and 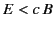 holds in all frames or in none.
holds in all frames or in none.
 then the field is said to be null. For a null field,
then the field is said to be null. For a null field,
 is perpendicular to
is perpendicular to  , and
, and 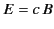 , in all frames.
, in all frames.
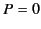 and
and 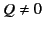 then there are infinitely many frames (with
a common relative direction of motion) in which
then there are infinitely many frames (with
a common relative direction of motion) in which 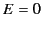 or
or 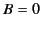 , according
as
, according
as 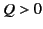 or
or 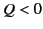 , and none other. Precisely one of these frames
moves in the direction
, and none other. Precisely one of these frames
moves in the direction
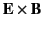 , its velocity being
, its velocity being
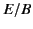 or
or
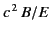 , respectively.
, respectively.
 then there are infinitely many frames (with a common
direction of motion) in which
then there are infinitely many frames (with a common
direction of motion) in which  is parallel to
is parallel to  , and
none other. Precisely one of these moves in the direction
, and
none other. Precisely one of these moves in the direction
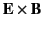 , its velocity being given by the smaller root of the quadratic
equation
, its velocity being given by the smaller root of the quadratic
equation
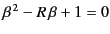 , where
, where 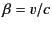 , and
, and
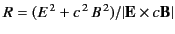 . In order for
. In order for  to be real
we require
to be real
we require 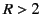 . Demonstrate that this is always the case.
. Demonstrate that this is always the case.
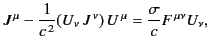
 is the 4-velocity of the medium,
is the 4-velocity of the medium, 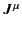 the
4-current, and
the
4-current, and
 the electromagnetic field tensor.
the electromagnetic field tensor.

 with
respect to some inertial frame then the 3-vector current in that frame
is
with
respect to some inertial frame then the 3-vector current in that frame
is
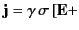

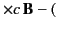

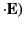

![$\displaystyle ] +\rho \,{\bf v}
$](img4203.png)
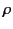 is the charge density observed in the inertial frame.
is the charge density observed in the inertial frame.


![$\displaystyle \frac{dP(t')}{d{\mit\Omega}} = \frac{e^{\,2}\,c \,\beta^{\,4}}{16...
...ta \,\cos^2(\omega_0 \,t')}{[1+\beta\,\cos\theta \,\sin(\omega_0 \,t')]^{\,5}}
$](img4214.png)
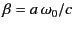 , and
, and  is a standard spherical polar
coordinate.
is a standard spherical polar
coordinate.
![$\displaystyle \frac{dP}{d{\mit\Omega}} = \frac{e^{\,2} \,c\, \beta^{\,4}}{128\p...
...,2}\,\cos^2\theta}{(1-\beta^{\,2}\,\cos^2\theta)^{\,7/2}}\right] \sin^2\theta.
$](img4216.png)