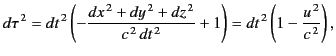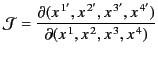Next: 4-Velocity and 4-Acceleration
Up: Relativity and Electromagnetism
Previous: Space-Time
It is often helpful to write the invariant differential interval 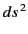 in
the form
in
the form
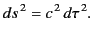 |
(1714) |
The quantity 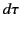 is called the proper time. It follows that
is called the proper time. It follows that
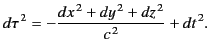 |
(1715) |
Consider a series of events on the world-line of some material
particle. If the particle has speed 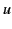 then
then
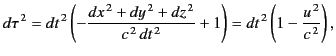 |
(1716) |
implying that
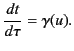 |
(1717) |
It is clear that 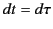 in the particle's
rest frame. Thus,
in the particle's
rest frame. Thus, 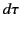 corresponds to the
time difference between two neighboring events on the particle's world-line,
as measured by a clock attached to the particle (hence, the name ``proper
time''). According to Equation (1719), the particle's clock appears to run slow,
by a factor
corresponds to the
time difference between two neighboring events on the particle's world-line,
as measured by a clock attached to the particle (hence, the name ``proper
time''). According to Equation (1719), the particle's clock appears to run slow,
by a factor 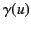 , in an inertial frame
in which the particle is moving with velocity
, in an inertial frame
in which the particle is moving with velocity 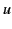 . This is the celebrated time dilation
effect.
. This is the celebrated time dilation
effect.
Let us consider how a small 4-dimensional volume element
in space-time transforms under
a general Lorentz transformation. We have
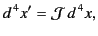 |
(1718) |
where
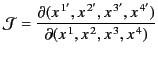 |
(1719) |
is the Jacobian of the transformation: that is, the determinant of
the transformation matrix
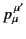 . A general Lorentz transformation
is made up of a standard Lorentz transformation plus a displacement and
a rotation. Thus, the transformation matrix is the product of
that for a standard Lorentz transformation, a translation, and a rotation.
It follows that the Jacobian of a general Lorentz transformation
is the product of that for a standard Lorentz transformation, a translation,
and a rotation. It is well known that the Jacobians of the latter two
transformations are unity, because they are both volume preserving transformations
that do not affect time. Likewise, it is easily seen
[e.g.,
by taking the determinant of the transformation matrix (1698)]
that the Jacobian of a standard Lorentz transformation is also unity.
It follows that
. A general Lorentz transformation
is made up of a standard Lorentz transformation plus a displacement and
a rotation. Thus, the transformation matrix is the product of
that for a standard Lorentz transformation, a translation, and a rotation.
It follows that the Jacobian of a general Lorentz transformation
is the product of that for a standard Lorentz transformation, a translation,
and a rotation. It is well known that the Jacobians of the latter two
transformations are unity, because they are both volume preserving transformations
that do not affect time. Likewise, it is easily seen
[e.g.,
by taking the determinant of the transformation matrix (1698)]
that the Jacobian of a standard Lorentz transformation is also unity.
It follows that
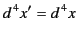 |
(1720) |
for a general Lorentz transformation. In other words, a general Lorentz
transformation preserves the volume of space-time. Because time is dilated by
a factor 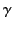 in
a moving frame, the volume of space-time
can only be preserved if the volume of
ordinary 3-space is reduced by the same factor. As is well-known, this
is achieved by length contraction along the
direction of motion by a factor
in
a moving frame, the volume of space-time
can only be preserved if the volume of
ordinary 3-space is reduced by the same factor. As is well-known, this
is achieved by length contraction along the
direction of motion by a factor 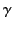 .
.



Next: 4-Velocity and 4-Acceleration
Up: Relativity and Electromagnetism
Previous: Space-Time
Richard Fitzpatrick
2014-06-27
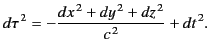
![]() then
then