


Next: Relativity and Electromagnetism
Up: Multipole Expansion
Previous: Mie Scattering
- An almost spherical surface defined by
has inside it a uniform volume distribution of charge totaling 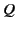 . The small parameter
. The small parameter  varies harmonically in time at the angular frequency
varies harmonically in time at the angular frequency  . This corresponds to a surface waves
on a sphere. Keeping only the lowest-order terms in
. This corresponds to a surface waves
on a sphere. Keeping only the lowest-order terms in  , and making the long-wavelength approximation,
calculate the nonvanishing multipole moments, the angular distribution of radiation, and the total
radiated power.
, and making the long-wavelength approximation,
calculate the nonvanishing multipole moments, the angular distribution of radiation, and the total
radiated power.
- The uniform charge density of the previous exercise is replaced by a uniform magnetization parallel
to the
 -axis and having a total magnetic moment
-axis and having a total magnetic moment  . With the same approximations as in the previous
exercise, calculate the nonvanishing multipole moments, the angular distribution of radiation, and the total
radiated power.
. With the same approximations as in the previous
exercise, calculate the nonvanishing multipole moments, the angular distribution of radiation, and the total
radiated power.
Richard Fitzpatrick
2014-06-27