


Next: Electromagnetic Momentum Conservation
Up: Maxwell's Equations
Previous: Retarded Fields
Electromagnetic Energy Conservation
Consider the fourth Maxwell equation:
 |
(100) |
Forming the scalar product with the electric field, and rearranging, we obtain
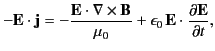 |
(101) |
which can be rewritten
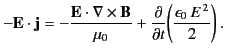 |
(102) |
Now,
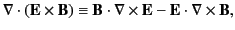 |
(103) |
so
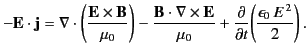 |
(104) |
Making use of third Maxwell equation,
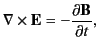 |
(105) |
we obtain
 |
(106) |
which can be rewritten
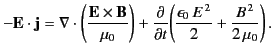 |
(107) |
Thus, we get
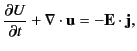 |
(108) |
where 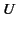 and
and 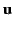 are specified in Equations (109) and (110), respectively.
are specified in Equations (109) and (110), respectively.
By comparison with Equation (7), we can recognize the previous expression as some sort of conservation equation.
Here, 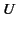 is the density of the conserved quantity,
is the density of the conserved quantity, 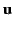 is the flux of the conserved quantity, and
is the flux of the conserved quantity, and
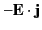 is the
rate at which the conserved quantity is created per unit volume. However,
is the
rate at which the conserved quantity is created per unit volume. However,
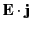 is the rate per unit volume at which electric charges
gain energy via interaction with electromagnetic fields. Hence,
is the rate per unit volume at which electric charges
gain energy via interaction with electromagnetic fields. Hence,
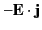 is the rate per unit volume at which electromagnetic
fields gain energy via interaction with charges. It follows that Equation (108) is a conservation equation for electromagnetic energy.
Thus.
is the rate per unit volume at which electromagnetic
fields gain energy via interaction with charges. It follows that Equation (108) is a conservation equation for electromagnetic energy.
Thus.
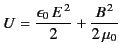 |
(109) |
can be interpreted as the electromagnetic energy density,
and
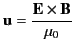 |
(110) |
as the electromagnetic energy flux. The latter quantity is usually called the
Poynting flux, after its discoverer.



Next: Electromagnetic Momentum Conservation
Up: Maxwell's Equations
Previous: Retarded Fields
Richard Fitzpatrick
2014-06-27


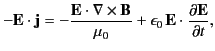
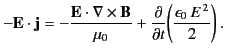
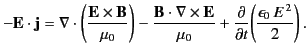
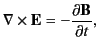

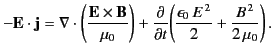
![]() is the density of the conserved quantity,
is the density of the conserved quantity, ![]() is the flux of the conserved quantity, and
is the flux of the conserved quantity, and
![]() is the
rate at which the conserved quantity is created per unit volume. However,
is the
rate at which the conserved quantity is created per unit volume. However,
![]() is the rate per unit volume at which electric charges
gain energy via interaction with electromagnetic fields. Hence,
is the rate per unit volume at which electric charges
gain energy via interaction with electromagnetic fields. Hence,
![]() is the rate per unit volume at which electromagnetic
fields gain energy via interaction with charges. It follows that Equation (108) is a conservation equation for electromagnetic energy.
Thus.
is the rate per unit volume at which electromagnetic
fields gain energy via interaction with charges. It follows that Equation (108) is a conservation equation for electromagnetic energy.
Thus.