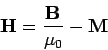Next: Magnetic susceptibility and permeability
Up: Dielectric and magnetic media
Previous: Energy density within a
All matter is built up out of atoms, and each atom consists of
electrons in motion. The currents
associated with this motion
are termed atomic currents. Each atomic current is
a tiny closed circuit of atomic dimensions, and may therefore be
appropriately described as a magnetic dipole. If the atomic currents
of a given atom all flow in the same plane then the atomic dipole moment is directed normal
to the plane (in the sense given by the right-hand rule), and its magnitude
is the product of the total circulating current and the area of the
current loop. More generally, if
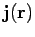 is the atomic current
density at the point
is the atomic current
density at the point 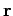 then the magnetic moment of the atom
is
then the magnetic moment of the atom
is
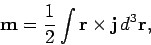 |
(856) |
where the integral is over the volume of the atom. If there are  such
atoms or molecules per unit volume then the magnetization
such
atoms or molecules per unit volume then the magnetization 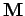 (i.e., the magnetic dipole moment per unit volume) is given
by
(i.e., the magnetic dipole moment per unit volume) is given
by
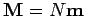 . More generally,
. More generally,
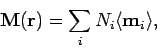 |
(857) |
where
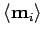 is the average magnetic dipole moment
of the
is the average magnetic dipole moment
of the 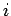 th type of molecule in the vicinity of point
th type of molecule in the vicinity of point 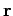 ,
and
,
and 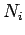 is the average number of such molecules per unit volume at
is the average number of such molecules per unit volume at
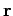 .
.
Consider a general medium which is made up of molecules which are
polarizable and possess a net magnetic moment.
It is easily demonstrated that any circulation in the magnetization field
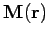 gives rise to an effective current density
gives rise to an effective current density
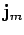 in the medium. In fact,
in the medium. In fact,
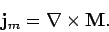 |
(858) |
This current density is called the magnetization current density,
and is usually distinguished from the true current density,
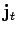 , which represents the convection of free charges in the
medium. In fact, there is a third type of current called a polarization
current, which is due to the apparent convection of bound charges.
It is easily demonstrated that the polarization current density,
, which represents the convection of free charges in the
medium. In fact, there is a third type of current called a polarization
current, which is due to the apparent convection of bound charges.
It is easily demonstrated that the polarization current density,
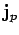 , is given by
, is given by
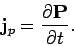 |
(859) |
Thus, the total current density, 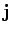 , in the medium takes the form
, in the medium takes the form
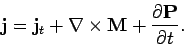 |
(860) |
It must be emphasized that all terms on the right-hand side of
the above equation represent
real physical currents, although only the first term is due to the motion
of real charges (over more than atomic dimensions).
The differential form of Ampère's law is
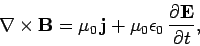 |
(861) |
which can also be written
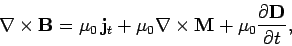 |
(862) |
where use has been made of the definition
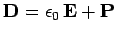 . The above expression can be rearranged to give
. The above expression can be rearranged to give
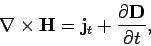 |
(863) |
where
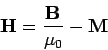 |
(864) |
is termed the magnetic intensity, and has the same dimensions
as 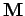 (i.e., magnetic dipole moment per unit volume).
In a steady-state situation, Stokes' theorem tell us that
(i.e., magnetic dipole moment per unit volume).
In a steady-state situation, Stokes' theorem tell us that
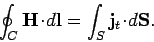 |
(865) |
In other words, the line integral of  around some closed curve
is equal to the flux of true current through any surface attached to that
curve. Unlike the magnetic field
around some closed curve
is equal to the flux of true current through any surface attached to that
curve. Unlike the magnetic field 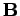 (which specifies
the force
(which specifies
the force
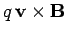 acting on a charge
acting on a charge 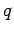 moving
with velocity
moving
with velocity 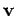 ),
or the magnetization
),
or the magnetization 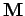 (the magnetic dipole moment
per unit volume), the magnetic intensity
(the magnetic dipole moment
per unit volume), the magnetic intensity  has no clear physical
meaning. The only reason for introducing it is that it enables us to
calculate fields in the presence of magnetic materials without
first having to know the distribution of magnetization currents.
However, this is only possible if we possess a constitutive relation
connecting
has no clear physical
meaning. The only reason for introducing it is that it enables us to
calculate fields in the presence of magnetic materials without
first having to know the distribution of magnetization currents.
However, this is only possible if we possess a constitutive relation
connecting 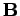 and
and  .
.



Next: Magnetic susceptibility and permeability
Up: Dielectric and magnetic media
Previous: Energy density within a
Richard Fitzpatrick
2006-02-02
![]() gives rise to an effective current density
gives rise to an effective current density
![]() in the medium. In fact,
in the medium. In fact,