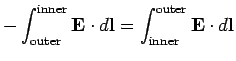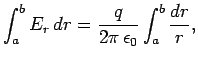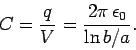Next: Poisson's equation
Up: Electrostatics
Previous: Boundary conditions on the
Capacitors
We can store electrical
charge on the surface of a conductor. However,
electric fields will be generated immediately above this surface.
The conductor can only successfully store charge if it is electrically insulated
from its surroundings. Air is a very good insulator. Unfortunately, air
ceases to be an insulator when the electric field-strength through it exceeds some
critical value which is about
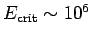 volts per meter. This
phenomenon, which is called break-down, is associated with the formation
of sparks. The most well-known example of the break-down of
air is during a lightning
strike. Clearly, a good charge storing device is one which holds a large amount
of charge but only generates small electric fields. Such a device is called
a capacitor.
volts per meter. This
phenomenon, which is called break-down, is associated with the formation
of sparks. The most well-known example of the break-down of
air is during a lightning
strike. Clearly, a good charge storing device is one which holds a large amount
of charge but only generates small electric fields. Such a device is called
a capacitor.
Consider two thin, parallel, conducting
plates of cross-sectional area 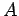 which are separated by
a small distance
which are separated by
a small distance 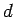 (i.e.,
(i.e., 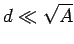 ). Suppose that each plate
carries an equal and opposite charge
). Suppose that each plate
carries an equal and opposite charge  . We expect this charge to
spread evenly over the plates to give an effective sheet charge density
. We expect this charge to
spread evenly over the plates to give an effective sheet charge density
 on each plate. Suppose that the upper plate carries a
positive charge and that the lower plate carries a negative charge. According to
Eqs. (624) and (625), the field generated by the upper plate is normal to the plate and
of magnitude
on each plate. Suppose that the upper plate carries a
positive charge and that the lower plate carries a negative charge. According to
Eqs. (624) and (625), the field generated by the upper plate is normal to the plate and
of magnitude
Likewise, the field generated by the lower plate is
Note that we are neglecting any ``leakage'' of the field at the edges of the plates.
This is reasonable if the plates are closely spaced. The total field is the
sum of the two fields generated by the upper and lower plates. Thus, the net field
is normal to the plates, and of magnitude
Since the electric field is uniform, the potential difference between the
plates is simply
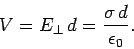 |
(644) |
It is conventional to measure the capacity of a conductor, or set of conductors,
to store charge, but generate small electric fields, in terms of a parameter
called the capacitance. This is
usually denoted  . The capacitance of a charge storing
device is simply the ratio of the charge stored to the potential difference
generated by the charge. Thus,
. The capacitance of a charge storing
device is simply the ratio of the charge stored to the potential difference
generated by the charge. Thus,
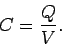 |
(645) |
Clearly, a good charge storing device has a high capacitance. Incidentally,
capacitance is measured in coulombs per volt, or farads. This is a rather unwieldy
unit, since
good capacitors typically have capacitances which are only about one millionth
of a farad. For a parallel plate capacitor, it is clear that
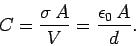 |
(646) |
Note that the capacitance only depends on geometric quantities, such as the area
and spacing of the plates. This is a consequence of the superposability of
electric fields. If we double the charge on conductors then we double
the electric fields generated around them, and we, therefore, double the potential
difference between the conductors. Thus, the potential difference between
the conductors is always directly proportional to the charge carried:
the constant
of proportionality (the inverse of the capacitance) can only depend on geometry.
Suppose that the charge 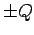 on each plate is built up gradually by transferring
small amounts of charge from one plate to another. If the
instantaneous charge on the plates is
on each plate is built up gradually by transferring
small amounts of charge from one plate to another. If the
instantaneous charge on the plates is  , and an infinitesimal amount of
positive
charge
, and an infinitesimal amount of
positive
charge 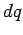 is transferred from the negatively charged plate to the positively
charge plate, then the work done is
is transferred from the negatively charged plate to the positively
charge plate, then the work done is
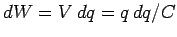 ,
where
,
where  is the instantaneous
voltage difference between the plates. Note that the voltage difference is such
that it opposes any increase in the charge on either plate.
The total work done in charging the capacitor
is
is the instantaneous
voltage difference between the plates. Note that the voltage difference is such
that it opposes any increase in the charge on either plate.
The total work done in charging the capacitor
is
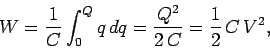 |
(647) |
where use has been made of Eq. (645).
The energy stored in the capacitor is the same as the work required to
charge up the capacitor. Thus,
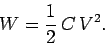 |
(648) |
This is a general result which holds for all types of capacitor.
The energy of
a charged parallel
plate
capacitor is actually stored in the electric field between the plates. This field
is of approximately constant magnitude 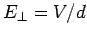 , and occupies a
region of volume
, and occupies a
region of volume  . Thus, given the energy density of an electric
field,
. Thus, given the energy density of an electric
field,
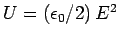 , the energy stored in the
electric field is
, the energy stored in the
electric field is
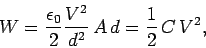 |
(649) |
where use has been made of Eq. (646).
Note that Eqs. (647) and (649) agree. We all know that if we connect a capacitor
across the terminals of a battery then a transient current flows as the capacitor
charges up. The capacitor can then be placed to one side, and, some time later,
the stored charge can be used: for instance, to transiently light a bulb in
an electrical circuit. What is interesting here is that the energy stored in the
capacitor is stored as an electric field, so we can think of a capacitor as a
device which either
stores energy in, or extracts energy from, an electric
field.
The idea, which we discussed earlier, that an electric field exerts a negative
pressure
 on conductors immediately suggests that
the two plates in a parallel plate capacitor attract one another with a
mutual force
on conductors immediately suggests that
the two plates in a parallel plate capacitor attract one another with a
mutual force
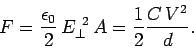 |
(650) |
It is not necessary to have two oppositely charged conductors
in order to make a capacitor.
Consider an isolated
sphere of radius  which
carries a charge
which
carries a charge  . The radial electric field generated outside the sphere is
given by
. The radial electric field generated outside the sphere is
given by
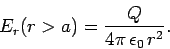 |
(651) |
The potential difference between the sphere and infinity, or, more realistically,
some large, relatively distant reservoir of charge such as the Earth, is
 |
(652) |
Thus, the capacitance of the sphere is
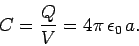 |
(653) |
The energy of a sphere when it carries a charge  is again given by
is again given by
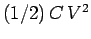 . It can easily be demonstrated that this is really
the energy contained in the electric field around the sphere.
. It can easily be demonstrated that this is really
the energy contained in the electric field around the sphere.
Suppose that we have two spheres of radii  and
and  , respectively, which are
connected by an electric wire. The wire allows charge to move back and forth between
the spheres until they reach the same potential (with respect to infinity).
Let
, respectively, which are
connected by an electric wire. The wire allows charge to move back and forth between
the spheres until they reach the same potential (with respect to infinity).
Let  be the charge on the first sphere and
be the charge on the first sphere and 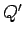 the charge on the
second sphere.
Of course, the total charge
the charge on the
second sphere.
Of course, the total charge 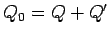 carried by the two spheres is a conserved
quantity. It follows from Eq. (652) that
carried by the two spheres is a conserved
quantity. It follows from Eq. (652) that
Note that if one sphere is much smaller than the other one, e.g., 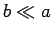 , then
the large sphere grabs most of the charge:
, then
the large sphere grabs most of the charge:
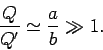 |
(656) |
The ratio of the electric fields generated just above the surfaces of the two
spheres follows from Eqs. (651) and (656):
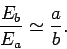 |
(657) |
If 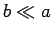 , then the field just above the smaller sphere
is far larger than that above the larger sphere.
Equation (657) is a simple example of a far more general rule.
The electric field above some point on the
surface of a conductor is inversely proportional to
the local radius of curvature of the surface.
, then the field just above the smaller sphere
is far larger than that above the larger sphere.
Equation (657) is a simple example of a far more general rule.
The electric field above some point on the
surface of a conductor is inversely proportional to
the local radius of curvature of the surface.
It is clear that if we wish to store significant amounts of charge on a conductor
then the surface of the conductor must be made as smooth as possible. Any sharp
spikes on the surface will inevitably
have comparatively small radii of curvature. Intense local electric fields are
generated in these regions.
These can easily exceed the critical field for the break-down of air,
leading to sparking and the eventual loss of the charge on the conductor.
Sparking can also be very destructive because the associated
electric currents flow through very localized
regions giving rise to intense ohmic heating.
As a final example, consider two co-axial
conducting cylinders of radii  and
and
 , where
, where 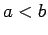 . Suppose that the charge per unit length carried by the
outer and inner cylinders is
. Suppose that the charge per unit length carried by the
outer and inner cylinders is 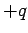 and
and 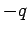 , respectively. We can safely
assume that
, respectively. We can safely
assume that
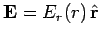 , by symmetry (adopting
standard cylindrical polar coordinates). Let us apply
Gauss' law to a cylinder of radius
, by symmetry (adopting
standard cylindrical polar coordinates). Let us apply
Gauss' law to a cylinder of radius 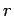 , co-axial with the conductors, and
of length
, co-axial with the conductors, and
of length  . For
. For 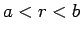 , we find that
, we find that
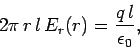 |
(658) |
so
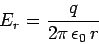 |
(659) |
for 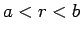 . It is fairly obvious that
. It is fairly obvious that  if
if 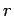 is not in the range
is not in the range
 to
to  . The potential difference between the inner and outer cylinders is
. The potential difference between the inner and outer cylinders is
so
 |
(661) |
Thus, the capacitance per unit length of the two cylinders is
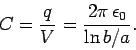 |
(662) |



Next: Poisson's equation
Up: Electrostatics
Previous: Boundary conditions on the
Richard Fitzpatrick
2006-02-02
![]() which are separated by
a small distance
which are separated by
a small distance ![]() (i.e.,
(i.e., ![]() ). Suppose that each plate
carries an equal and opposite charge
). Suppose that each plate
carries an equal and opposite charge ![]() . We expect this charge to
spread evenly over the plates to give an effective sheet charge density
. We expect this charge to
spread evenly over the plates to give an effective sheet charge density
![]() on each plate. Suppose that the upper plate carries a
positive charge and that the lower plate carries a negative charge. According to
Eqs. (624) and (625), the field generated by the upper plate is normal to the plate and
of magnitude
on each plate. Suppose that the upper plate carries a
positive charge and that the lower plate carries a negative charge. According to
Eqs. (624) and (625), the field generated by the upper plate is normal to the plate and
of magnitude





![]() on each plate is built up gradually by transferring
small amounts of charge from one plate to another. If the
instantaneous charge on the plates is
on each plate is built up gradually by transferring
small amounts of charge from one plate to another. If the
instantaneous charge on the plates is ![]() , and an infinitesimal amount of
positive
charge
, and an infinitesimal amount of
positive
charge ![]() is transferred from the negatively charged plate to the positively
charge plate, then the work done is
is transferred from the negatively charged plate to the positively
charge plate, then the work done is
![]() ,
where
,
where ![]() is the instantaneous
voltage difference between the plates. Note that the voltage difference is such
that it opposes any increase in the charge on either plate.
The total work done in charging the capacitor
is
is the instantaneous
voltage difference between the plates. Note that the voltage difference is such
that it opposes any increase in the charge on either plate.
The total work done in charging the capacitor
is
![]() , and occupies a
region of volume
, and occupies a
region of volume ![]() . Thus, given the energy density of an electric
field,
. Thus, given the energy density of an electric
field,
![]() , the energy stored in the
electric field is
, the energy stored in the
electric field is
![]() on conductors immediately suggests that
the two plates in a parallel plate capacitor attract one another with a
mutual force
on conductors immediately suggests that
the two plates in a parallel plate capacitor attract one another with a
mutual force
![]() which
carries a charge
which
carries a charge ![]() . The radial electric field generated outside the sphere is
given by
. The radial electric field generated outside the sphere is
given by
![]() and
and ![]() , respectively, which are
connected by an electric wire. The wire allows charge to move back and forth between
the spheres until they reach the same potential (with respect to infinity).
Let
, respectively, which are
connected by an electric wire. The wire allows charge to move back and forth between
the spheres until they reach the same potential (with respect to infinity).
Let ![]() be the charge on the first sphere and
be the charge on the first sphere and ![]() the charge on the
second sphere.
Of course, the total charge
the charge on the
second sphere.
Of course, the total charge ![]() carried by the two spheres is a conserved
quantity. It follows from Eq. (652) that
carried by the two spheres is a conserved
quantity. It follows from Eq. (652) that
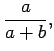
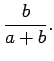
![]() and
and
![]() , where
, where ![]() . Suppose that the charge per unit length carried by the
outer and inner cylinders is
. Suppose that the charge per unit length carried by the
outer and inner cylinders is ![]() and
and ![]() , respectively. We can safely
assume that
, respectively. We can safely
assume that
![]() , by symmetry (adopting
standard cylindrical polar coordinates). Let us apply
Gauss' law to a cylinder of radius
, by symmetry (adopting
standard cylindrical polar coordinates). Let us apply
Gauss' law to a cylinder of radius ![]() , co-axial with the conductors, and
of length
, co-axial with the conductors, and
of length ![]() . For
. For ![]() , we find that
, we find that