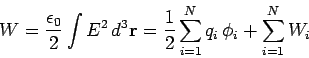Next: Ohm's law
Up: Electrostatics
Previous: Introduction
Consider a collection of 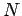 static point charges
static point charges 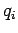 located at position vectors
located at position vectors
 (where
(where 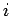 runs from 1 to
runs from 1 to 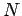 ).
What is the electrostatic energy stored in such a collection? Another way
of asking this is, how much work would we have to do in order to assemble
the charges, starting from an initial state in which they are all
at rest and very widely
separated?
).
What is the electrostatic energy stored in such a collection? Another way
of asking this is, how much work would we have to do in order to assemble
the charges, starting from an initial state in which they are all
at rest and very widely
separated?
We know that a static electric field is conservative, and can consequently
be written in terms of
a scalar potential:
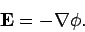 |
(576) |
We also know that the electric force on a charge 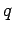 is
written
is
written
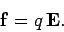 |
(577) |
The work we would have to do against electrical forces in order to
move the charge from point  to point
to point  is simply
is simply
![\begin{displaymath}
W =- \int_P^Q {\bf f} \cdot d{\bf l} =- q \int_P^Q {\bf E} \...
...\nabla\phi \cdot d{\bf l} = q \left[ \phi(Q) - \phi(P)\right].
\end{displaymath}](img1235.png) |
(578) |
The negative sign in the above expression comes about because we would have to
exert a force 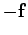 on the charge, in order to counteract the force
exerted by the electric field. Recall that the scalar potential
generated by a point charge
on the charge, in order to counteract the force
exerted by the electric field. Recall that the scalar potential
generated by a point charge 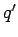 at position
at position 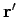 is
is
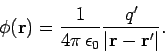 |
(579) |
Let us build up our collection of charges one by one. It takes no work to bring the
first charge from infinity, since there is no electric field to fight against.
Let us clamp this charge in position at 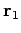 . In order to bring the
second charge into position at
. In order to bring the
second charge into position at 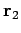 ,
we have to do work against the electric field
generated by the first charge. According to Eqs. (578) and Eqs. (579),
this work is given by
,
we have to do work against the electric field
generated by the first charge. According to Eqs. (578) and Eqs. (579),
this work is given by
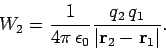 |
(580) |
Let us now bring the third charge into position. Since electric fields
and scalar potentials are
superposable, the work done whilst moving the third charge from infinity to 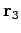 is simply the sum of the works done against the electric fields generated by
charges 1 and 2 taken in isolation:
is simply the sum of the works done against the electric fields generated by
charges 1 and 2 taken in isolation:
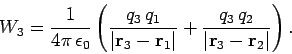 |
(581) |
Thus, the total work done in assembling the three charges is given by
 |
(582) |
This result can easily be generalized to 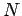 charges:
charges:
 |
(583) |
The restriction that 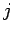 must be less than
must be less than 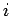 makes the above summation
rather messy. If we were to sum without restriction (other than
makes the above summation
rather messy. If we were to sum without restriction (other than 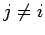 ) then
each pair of charges would be counted twice. It is convenient to do just
this, and then to divide the result by two. Thus,
) then
each pair of charges would be counted twice. It is convenient to do just
this, and then to divide the result by two. Thus,
 |
(584) |
This is the potential energy (i.e., the difference between the total energy
and the kinetic energy) of a collection of charges. We can think of this as the
work needed to bring static charges from infinity and assemble them in the
required formation. Alternatively, this is the kinetic energy which would
be released if the collection were dissolved, and the charges returned to infinity.
But where is this potential energy stored? Let us investigate further.
Equation (584) can be written
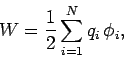 |
(585) |
where
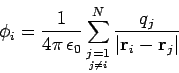 |
(586) |
is the scalar potential experienced by the 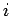 th charge due to the other
charges in the distribution.
th charge due to the other
charges in the distribution.
Let us now consider the potential energy of a continuous charge distribution.
It is tempting to write
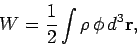 |
(587) |
by analogy with Eqs. (585) and (586), where
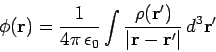 |
(588) |
is the familiar scalar potential generated by a continuous charge distribution.
Let us try this out. We know from Maxwell's equations that
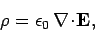 |
(589) |
so Eq. (587) can be written
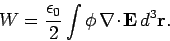 |
(590) |
Vector field theory yields the standard result
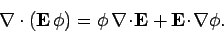 |
(591) |
However,
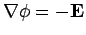 , so we obtain
, so we obtain
![\begin{displaymath}
W = \frac{\epsilon_0}{2} \left[\int \nabla\!\cdot \!({\bf E} \phi) d^3{\bf r}
+
\int E^2 d^3 {\bf r}\right]
\end{displaymath}](img1255.png) |
(592) |
Application of Gauss' theorem gives
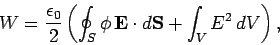 |
(593) |
where  is some volume which encloses all of the charges, and
is some volume which encloses all of the charges, and  is its bounding
surface. Let us assume that
is its bounding
surface. Let us assume that  is a sphere, centred on the origin, and let
us take the limit in which the radius
is a sphere, centred on the origin, and let
us take the limit in which the radius  of this sphere goes to infinity.
We know that, in general, the electric field at large distances from a
bounded charge
distribution looks like the field of a point charge, and, therefore,
falls off like
of this sphere goes to infinity.
We know that, in general, the electric field at large distances from a
bounded charge
distribution looks like the field of a point charge, and, therefore,
falls off like 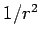 . Likewise, the potential falls off like
. Likewise, the potential falls off like 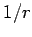 . However,
the surface area of the sphere increases like
. However,
the surface area of the sphere increases like  . Hence, it is clear that, in the
limit as
. Hence, it is clear that, in the
limit as
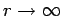 , the surface integral in Eq. (593) falls off
like
, the surface integral in Eq. (593) falls off
like 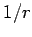 , and is consequently zero.
Thus, Eq. (593) reduces to
, and is consequently zero.
Thus, Eq. (593) reduces to
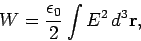 |
(594) |
where the integral is over all space. This is a very nice
result. It tells us that the potential energy of a continuous charge
distribution is stored in the electric field. Of course, we now have to assume that
an electric field possesses an energy density
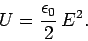 |
(595) |
We can easily check that Eq. (594) is correct. Suppose that we have a
charge  which is uniformly distributed within a sphere of
radius
which is uniformly distributed within a sphere of
radius  . Let us imagine building up this charge distribution
from a succession of thin spherical layers of infinitesimal thickness. At each
stage, we gather a small amount of charge from infinity, and spread it
over the surface of the sphere in a thin
layer from
. Let us imagine building up this charge distribution
from a succession of thin spherical layers of infinitesimal thickness. At each
stage, we gather a small amount of charge from infinity, and spread it
over the surface of the sphere in a thin
layer from 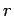 to
to 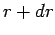 . We continue this process until the final radius of the
sphere is
. We continue this process until the final radius of the
sphere is  . If
. If  is the charge in the sphere when it has attained radius
is the charge in the sphere when it has attained radius
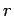 , then the work done in bringing a charge
, then the work done in bringing a charge 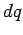 to it is
to it is
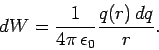 |
(596) |
This follows from Eq. (580), since the electric field generated by a spherical charge
distribution (outside itself)
is the same as that of a point charge  located at the origin
(
located at the origin
(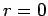 ) (see later). If the constant charge density in the sphere is
) (see later). If the constant charge density in the sphere is
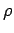 then
then
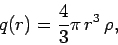 |
(597) |
and
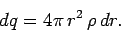 |
(598) |
Thus, Eq. (596) becomes
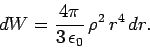 |
(599) |
The total work needed to build up the sphere from nothing to radius  is
plainly
is
plainly
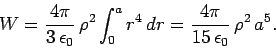 |
(600) |
This can also be written in terms of the total charge
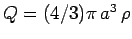 as
as
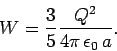 |
(601) |
Now that we have evaluated the potential energy of a spherical charge distribution
by the direct method, let us work it out using Eq. (594). We assume that the
electric field is radial and spherically symmetric, so
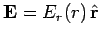 . Application of Gauss' law,
. Application of Gauss' law,
 |
(602) |
where  is a sphere of radius
is a sphere of radius 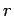 , yields
, yields
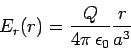 |
(603) |
for 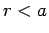 , and
, and
 |
(604) |
for 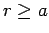 . Note that the electric field generated
outside the charge distribution is
the same as that of a point charge
. Note that the electric field generated
outside the charge distribution is
the same as that of a point charge  located at the origin,
located at the origin, 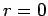 .
Equations (594), (603), and (604) yield
.
Equations (594), (603), and (604) yield
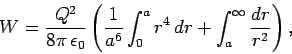 |
(605) |
which reduces to
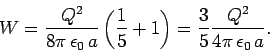 |
(606) |
Thus, Eq. (594) gives the correct answer.
The reason we have checked Eq. (594) so carefully is that on close inspection
it is found to be
inconsistent with Eq. (585), from which it was supposedly derived!
For instance, the energy given by Eq. (594) is manifestly positive definite, whereas
the energy given by Eq. (585) can be negative (it is certainly negative for
a collection of two point charges of opposite sign). The
inconsistency was introduced into our analysis when we replaced Eq. (586) by
Eq. (588). In Eq. (586), the self-interaction of the 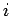 th charge with its
own electric field is specifically excluded, whereas it is included in Eq. (588). Thus,
the potential energies
(585) and (594) are different, because in the former we start from
ready-made point charges, whereas in the latter we build up the whole
charge distribution from scratch. Thus, if we were to work out the
potential energy of a point charge distribution using Eq. (594)
we would obtain the energy (585) plus the energy required to assemble the
point charges. What is the energy required to assemble a point charge?
In fact, it is infinite. To see this, let us suppose, for the sake of argument, that
our point charges are actually made of charge uniformly distributed over a small
sphere of radius
th charge with its
own electric field is specifically excluded, whereas it is included in Eq. (588). Thus,
the potential energies
(585) and (594) are different, because in the former we start from
ready-made point charges, whereas in the latter we build up the whole
charge distribution from scratch. Thus, if we were to work out the
potential energy of a point charge distribution using Eq. (594)
we would obtain the energy (585) plus the energy required to assemble the
point charges. What is the energy required to assemble a point charge?
In fact, it is infinite. To see this, let us suppose, for the sake of argument, that
our point charges are actually made of charge uniformly distributed over a small
sphere of radius  . According to Eq. (601), the energy required to assemble the
. According to Eq. (601), the energy required to assemble the
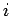 th point charge is
th point charge is
 |
(607) |
We can think of this as the self-energy of the 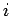 th charge.
Thus, we can write
th charge.
Thus, we can write
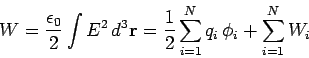 |
(608) |
which enables us to reconcile Eqs. (585) and (594). Unfortunately, if
our point charges really are point charges then
 , and the
self-energy of each charge becomes infinite. Thus, the potential
energies predicted by Eqs. (585) and (594) differ by an infinite amount.
What does this all mean? We have to conclude that the idea of locating electrostatic
potential energy in the electric field is inconsistent with the existence of point charges. One way out of this difficulty would be to
say that all elementary charges, such as electrons, are not points, but instead
small distributions of charge. Alternatively, we could say that our classical
theory of electromagnetism breaks down on very small length-scales due to
quantum effects. Unfortunately, the quantum mechanical version of electromagnetism
(quantum electrodynamics, or QED, for short)
suffers from the same infinities in the self-energies of particles as the classical
version. There is a prescription, called renormalization, for steering round these
infinities, and getting finite answers which agree with experiments to
extraordinary accuracy. However, nobody really understands why this prescription
works. The problem of the
infinite self-energies of elementary charged particles is still unresolved.
, and the
self-energy of each charge becomes infinite. Thus, the potential
energies predicted by Eqs. (585) and (594) differ by an infinite amount.
What does this all mean? We have to conclude that the idea of locating electrostatic
potential energy in the electric field is inconsistent with the existence of point charges. One way out of this difficulty would be to
say that all elementary charges, such as electrons, are not points, but instead
small distributions of charge. Alternatively, we could say that our classical
theory of electromagnetism breaks down on very small length-scales due to
quantum effects. Unfortunately, the quantum mechanical version of electromagnetism
(quantum electrodynamics, or QED, for short)
suffers from the same infinities in the self-energies of particles as the classical
version. There is a prescription, called renormalization, for steering round these
infinities, and getting finite answers which agree with experiments to
extraordinary accuracy. However, nobody really understands why this prescription
works. The problem of the
infinite self-energies of elementary charged particles is still unresolved.



Next: Ohm's law
Up: Electrostatics
Previous: Introduction
Richard Fitzpatrick
2006-02-02
![]() . In order to bring the
second charge into position at
. In order to bring the
second charge into position at ![]() ,
we have to do work against the electric field
generated by the first charge. According to Eqs. (578) and Eqs. (579),
this work is given by
,
we have to do work against the electric field
generated by the first charge. According to Eqs. (578) and Eqs. (579),
this work is given by
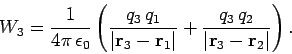


![]() which is uniformly distributed within a sphere of
radius
which is uniformly distributed within a sphere of
radius ![]() . Let us imagine building up this charge distribution
from a succession of thin spherical layers of infinitesimal thickness. At each
stage, we gather a small amount of charge from infinity, and spread it
over the surface of the sphere in a thin
layer from
. Let us imagine building up this charge distribution
from a succession of thin spherical layers of infinitesimal thickness. At each
stage, we gather a small amount of charge from infinity, and spread it
over the surface of the sphere in a thin
layer from ![]() to
to ![]() . We continue this process until the final radius of the
sphere is
. We continue this process until the final radius of the
sphere is ![]() . If
. If ![]() is the charge in the sphere when it has attained radius
is the charge in the sphere when it has attained radius
![]() , then the work done in bringing a charge
, then the work done in bringing a charge ![]() to it is
to it is
![]() . Application of Gauss' law,
. Application of Gauss' law,
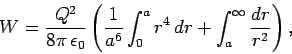
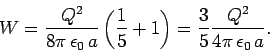
![]() th charge with its
own electric field is specifically excluded, whereas it is included in Eq. (588). Thus,
the potential energies
(585) and (594) are different, because in the former we start from
ready-made point charges, whereas in the latter we build up the whole
charge distribution from scratch. Thus, if we were to work out the
potential energy of a point charge distribution using Eq. (594)
we would obtain the energy (585) plus the energy required to assemble the
point charges. What is the energy required to assemble a point charge?
In fact, it is infinite. To see this, let us suppose, for the sake of argument, that
our point charges are actually made of charge uniformly distributed over a small
sphere of radius
th charge with its
own electric field is specifically excluded, whereas it is included in Eq. (588). Thus,
the potential energies
(585) and (594) are different, because in the former we start from
ready-made point charges, whereas in the latter we build up the whole
charge distribution from scratch. Thus, if we were to work out the
potential energy of a point charge distribution using Eq. (594)
we would obtain the energy (585) plus the energy required to assemble the
point charges. What is the energy required to assemble a point charge?
In fact, it is infinite. To see this, let us suppose, for the sake of argument, that
our point charges are actually made of charge uniformly distributed over a small
sphere of radius ![]() . According to Eq. (601), the energy required to assemble the
. According to Eq. (601), the energy required to assemble the
![]() th point charge is
th point charge is