


Next: Ampère's law
Up: Time-independent Maxwell equations
Previous: Ampère's experiments
The Lorentz force
The flow of an electric current down
a conducting wire is ultimately due to the motion of
electrically charged particles
(in most cases, electrons) through the conducting medium.
It seems reasonable, therefore, that
the force exerted on the wire when it is placed in a magnetic field is really
the resultant of the forces exerted on these moving charges. Let us
suppose that this is the case.
Let 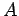 be the
(uniform) cross-sectional area of the wire, and let
be the
(uniform) cross-sectional area of the wire, and let 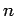 be the number density
of mobile charges in the conductor. Suppose that the
mobile charges each have charge
be the number density
of mobile charges in the conductor. Suppose that the
mobile charges each have charge 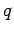 and velocity
and velocity 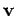 . We must assume that
the conductor also contains stationary charges, of charge
. We must assume that
the conductor also contains stationary charges, of charge 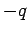 and number density
and number density
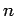 (say), so that the net charge density in the wire is zero. In most conductors, the
mobile charges are electrons and the stationary charges are atomic nuclei.
The magnitude of the electric current flowing through the wire is simply the
number of coulombs per second which flow past a given point. In one second,
a mobile charge moves a distance
(say), so that the net charge density in the wire is zero. In most conductors, the
mobile charges are electrons and the stationary charges are atomic nuclei.
The magnitude of the electric current flowing through the wire is simply the
number of coulombs per second which flow past a given point. In one second,
a mobile charge moves a distance 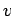 , so all of the charges contained in a
cylinder of cross-sectional area
, so all of the charges contained in a
cylinder of cross-sectional area 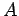 and length
and length 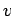 flow past a given point.
Thus, the magnitude of the current is
flow past a given point.
Thus, the magnitude of the current is 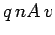 . The direction of the
current is the same as the direction of motion of the charges, so the
vector current is
. The direction of the
current is the same as the direction of motion of the charges, so the
vector current is
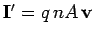 .
According to Eq. (229), the force per unit length acting on the wire is
.
According to Eq. (229), the force per unit length acting on the wire is
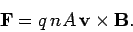 |
(232) |
However, a unit length of the wire contains 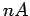 moving charges. So, assuming
that each charge is subject to an equal force from the magnetic field (we have
no reason to suppose otherwise), the force acting on an individual charge is
moving charges. So, assuming
that each charge is subject to an equal force from the magnetic field (we have
no reason to suppose otherwise), the force acting on an individual charge is
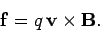 |
(233) |
We can combine this with Eq. (169) to give the force acting on a charge 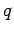 moving
with velocity
moving
with velocity 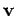 in an electric field
in an electric field 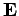 and a magnetic field
and a magnetic field
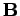 :
:
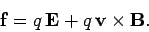 |
(234) |
This is called the Lorentz force law, after the Dutch physicist
Hendrik Antoon Lorentz who first formulated it. The electric
force on a charged particle is parallel to the local electric field.
The magnetic force, however, is perpendicular to both the local magnetic
field and the particle's direction of motion. No magnetic force is exerted on a
stationary charged particle.
The
equation of motion of a free particle of charge 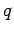 and
mass
and
mass 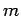 moving in electric and
magnetic fields is
moving in electric and
magnetic fields is
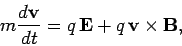 |
(235) |
according to the Lorentz force law.
This equation of motion was first verified in a famous experiment carried out
by the Cambridge physicist J.J. Thompson in 1897. Thompson was investigating
cathode rays, a then mysterious form of radiation emitted by a heated
metal element held at a large negative voltage (i.e., a cathode) with respect
to another metal element (i.e., an anode) in an evacuated tube.
German physicists held that cathode rays were
a form of electromagnetic radiation, whilst British and French physicists suspected
that they were, in reality, a stream of charged particles. Thompson was able to
demonstrate that the latter view was correct. In Thompson's experiment, the
cathode rays passed though a region of ``crossed'' electric and magnetic
fields (still in vacuum). The fields were perpendicular to the original
trajectory of the rays, and were also mutually perpendicular.
Let us analyze Thompson's experiment. Suppose that
the rays are originally traveling in the 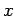 -direction, and are subject to
a uniform electric field
-direction, and are subject to
a uniform electric field 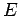 in the
in the 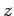 -direction and a uniform magnetic
field
-direction and a uniform magnetic
field 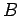 in the
in the 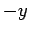 -direction. Let us assume, as Thompson did, that cathode
rays are a stream of particles of mass
-direction. Let us assume, as Thompson did, that cathode
rays are a stream of particles of mass 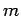 and charge
and charge 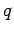 . The
equation of motion of the particles in the
. The
equation of motion of the particles in the 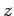 -direction is
-direction is
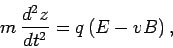 |
(236) |
where 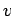 is the velocity of the particles in the
is the velocity of the particles in the 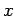 -direction.
Thompson started off his experiment by
only turning on the electric field in his apparatus, and
measuring the
deflection
-direction.
Thompson started off his experiment by
only turning on the electric field in his apparatus, and
measuring the
deflection 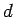 of the ray in the
of the ray in the 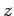 -direction after it had traveled a
distance
-direction after it had traveled a
distance 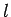 through the electric field. It is clear from the equation
of motion that
through the electric field. It is clear from the equation
of motion that
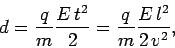 |
(237) |
where the ``time of flight'' 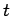 is replaced by
is replaced by 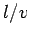 . This formula is only
valid if
. This formula is only
valid if 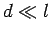 , which is assumed to be the case.
Next, Thompson turned on
the magnetic field in his apparatus, and adjusted it so that the cathode ray was
no longer deflected. The lack of deflection implies that the net force on the
particles in the
, which is assumed to be the case.
Next, Thompson turned on
the magnetic field in his apparatus, and adjusted it so that the cathode ray was
no longer deflected. The lack of deflection implies that the net force on the
particles in the 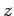 -direction was zero. In other words, the electric and
magnetic forces balanced exactly. It follows from Eq. (236)
that with a properly adjusted magnetic field strength
-direction was zero. In other words, the electric and
magnetic forces balanced exactly. It follows from Eq. (236)
that with a properly adjusted magnetic field strength
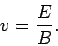 |
(238) |
Thus, Eqs. (237) and (238)
and can be combined and rearranged to give the charge to mass ratio of
the particles in terms of measured quantities:
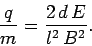 |
(239) |
Using this method, Thompson inferred that cathode rays were made up of
negatively charged particles (the sign of the charge is obvious from the
direction of the deflection in the electric field) with a charge to mass
ratio of
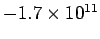 C/kg. A decade later, in 1908, the American Robert
Millikan performed his famous ``oil drop'' experiment, and discovered that
mobile electric charges are quantized in units of
C/kg. A decade later, in 1908, the American Robert
Millikan performed his famous ``oil drop'' experiment, and discovered that
mobile electric charges are quantized in units of
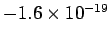 C.
Assuming that mobile electric charges and the particles which
make up cathode rays are one and the same thing,
Thompson's and Millikan's experiments imply that the mass
of these particles is
C.
Assuming that mobile electric charges and the particles which
make up cathode rays are one and the same thing,
Thompson's and Millikan's experiments imply that the mass
of these particles is
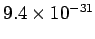 kg. Of course, this is the mass of
an electron (the modern value is
kg. Of course, this is the mass of
an electron (the modern value is
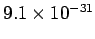 kg), and
kg), and
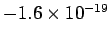 C is the charge of an electron. Thus, cathode rays are, in fact,
streams of electrons which are emitted from a heated cathode, and then
accelerated because of the large voltage difference between the cathode and anode.
C is the charge of an electron. Thus, cathode rays are, in fact,
streams of electrons which are emitted from a heated cathode, and then
accelerated because of the large voltage difference between the cathode and anode.
Consider, now, a particle of mass 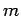 and charge
and charge 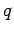 moving in a uniform
magnetic field,
moving in a uniform
magnetic field,
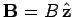 . According, to
Eq. (235), the particle's equation of motion can be written:
. According, to
Eq. (235), the particle's equation of motion can be written:
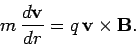 |
(240) |
This reduces to
Here,
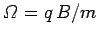 is called the cyclotron frequency.
The above equations can be solved to give
is called the cyclotron frequency.
The above equations can be solved to give
and
According to these equations, the particle trajectory is a spiral
whose axis is parallel to the magnetic field. The radius of the
spiral is
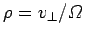 , where
, where 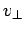 is the particle's
constant speed in the plane perpendicular to the magnetic field. The particle
drifts parallel to the magnetic field at a constant velocity,
is the particle's
constant speed in the plane perpendicular to the magnetic field. The particle
drifts parallel to the magnetic field at a constant velocity, 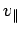 . Finally,
the particle gyrates in the plane perpendicular to the magnetic field at the cyclotron
frequency.
. Finally,
the particle gyrates in the plane perpendicular to the magnetic field at the cyclotron
frequency.
Finally, if a particle is subject to a force 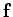 and moves a distance
and moves a distance
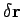 in a time interval
in a time interval 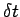 , then the work done on the particle by the
force is
, then the work done on the particle by the
force is
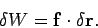 |
(250) |
The power input to the particle from the force field is
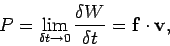 |
(251) |
where 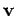 is the particle's velocity. It follows from the Lorentz force
law, Eq. (234), that the power input to a particle moving in electric and magnetic
fields is
is the particle's velocity. It follows from the Lorentz force
law, Eq. (234), that the power input to a particle moving in electric and magnetic
fields is
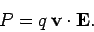 |
(252) |
Note that a charged particle can gain (or lose) energy from an electric
field, but not from a magnetic field. This is because the magnetic force is
always perpendicular to the particle's direction of motion, and, therefore, does
no work on the particle [see Eq. (250)]. Thus, in particle accelerators, magnetic
fields are often used to guide particle motion (e.g., in a circle) but the
actual acceleration is performed by electric fields.



Next: Ampère's law
Up: Time-independent Maxwell equations
Previous: Ampère's experiments
Richard Fitzpatrick
2006-02-02
![]() be the
(uniform) cross-sectional area of the wire, and let
be the
(uniform) cross-sectional area of the wire, and let ![]() be the number density
of mobile charges in the conductor. Suppose that the
mobile charges each have charge
be the number density
of mobile charges in the conductor. Suppose that the
mobile charges each have charge ![]() and velocity
and velocity ![]() . We must assume that
the conductor also contains stationary charges, of charge
. We must assume that
the conductor also contains stationary charges, of charge ![]() and number density
and number density
![]() (say), so that the net charge density in the wire is zero. In most conductors, the
mobile charges are electrons and the stationary charges are atomic nuclei.
The magnitude of the electric current flowing through the wire is simply the
number of coulombs per second which flow past a given point. In one second,
a mobile charge moves a distance
(say), so that the net charge density in the wire is zero. In most conductors, the
mobile charges are electrons and the stationary charges are atomic nuclei.
The magnitude of the electric current flowing through the wire is simply the
number of coulombs per second which flow past a given point. In one second,
a mobile charge moves a distance ![]() , so all of the charges contained in a
cylinder of cross-sectional area
, so all of the charges contained in a
cylinder of cross-sectional area ![]() and length
and length ![]() flow past a given point.
Thus, the magnitude of the current is
flow past a given point.
Thus, the magnitude of the current is ![]() . The direction of the
current is the same as the direction of motion of the charges, so the
vector current is
. The direction of the
current is the same as the direction of motion of the charges, so the
vector current is
![]() .
According to Eq. (229), the force per unit length acting on the wire is
.
According to Eq. (229), the force per unit length acting on the wire is
![]() and
mass
and
mass ![]() moving in electric and
magnetic fields is
moving in electric and
magnetic fields is
![]() -direction, and are subject to
a uniform electric field
-direction, and are subject to
a uniform electric field ![]() in the
in the ![]() -direction and a uniform magnetic
field
-direction and a uniform magnetic
field ![]() in the
in the ![]() -direction. Let us assume, as Thompson did, that cathode
rays are a stream of particles of mass
-direction. Let us assume, as Thompson did, that cathode
rays are a stream of particles of mass ![]() and charge
and charge ![]() . The
equation of motion of the particles in the
. The
equation of motion of the particles in the ![]() -direction is
-direction is
![]() and charge
and charge ![]() moving in a uniform
magnetic field,
moving in a uniform
magnetic field,
![]() . According, to
Eq. (235), the particle's equation of motion can be written:
. According, to
Eq. (235), the particle's equation of motion can be written:
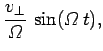
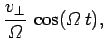
![]() and moves a distance
and moves a distance
![]() in a time interval
in a time interval ![]() , then the work done on the particle by the
force is
, then the work done on the particle by the
force is