


Next: Gauss' law
Up: Time-independent Maxwell equations
Previous: Coulomb's law
Suppose that
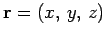 and
and
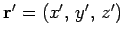 in Cartesian coordinates.
The
in Cartesian coordinates.
The  component of
component of
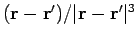 is
written
is
written
![\begin{displaymath}
\frac{x - x'}{[(x-x')^2+(y-y')^2 + (z-z')^2]^{ 3/2}}.
\end{displaymath}](img553.png) |
(173) |
However, it is easily demonstrated that
![$\displaystyle \frac{x - x'}{[(x-x')^2+(y-y')^2 + (z-z')^2]^{ 3/2}} = \mbox{\hspace{4cm}}$](img554.png) |
|
|
(174) |
![$\displaystyle \mbox{\hspace{4cm}}-\frac{\partial}{\partial x}\!\left(
\frac{1}{[(x-x')^2+(y-y')^2 + (z-z')^2]^{ 1/2}}\right).$](img555.png) |
|
|
|
Since there is nothing special about the  -axis, we can write
-axis, we can write
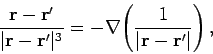 |
(175) |
where
 is a differential operator which involves the components of
is a differential operator which involves the components of 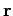 but not
those of
but not
those of 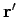 .
It follows from Eq. (172) that
.
It follows from Eq. (172) that
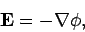 |
(176) |
where
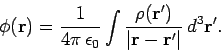 |
(177) |
Thus, the electric field generated by a collection of fixed charges can be written
as the gradient of a scalar potential, and this potential can be expressed as a
simple volume integral involving the charge distribution.
The scalar potential generated by a charge 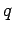 located at the origin is
located at the origin is
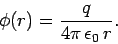 |
(178) |
According to Eq. (170), the scalar potential generated by a set of 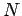 discrete charges
discrete charges 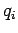 , located at
, located at  , is
, is
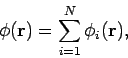 |
(179) |
where
 |
(180) |
Thus, the scalar potential is just the sum of the potentials generated by each
of the charges taken in isolation.
Suppose that a particle of
charge 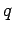 is taken along some path from point
is taken along some path from point  to point
to point  .
The net work done on the particle by electrical forces is
.
The net work done on the particle by electrical forces is
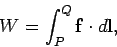 |
(181) |
where 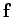 is the electrical force, and
is the electrical force, and 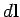 is a line element along the
path. Making use of Eqs. (169) and (176), we obtain
is a line element along the
path. Making use of Eqs. (169) and (176), we obtain
![\begin{displaymath}
W = q \int_P^Q {\bf E}\cdot d{\bf l} = - q\int_P^Q \nabla\phi\cdot d{\bf l}
= -q \left[ \phi(Q)- \phi(P) \right].
\end{displaymath}](img567.png) |
(182) |
Thus, the work done on the particle is simply minus its charge times the difference
in electric potential between the end point and the beginning point. This quantity
is clearly independent of the path taken between  and
and  . So, an electric field
generated by stationary charges is an example of a conservative field. In fact, this
result follows immediately from vector field theory once we are told,
in Eq. (176), that the electric field
is the gradient of a scalar potential. The work done on the particle
when it is taken around a closed loop is zero, so
. So, an electric field
generated by stationary charges is an example of a conservative field. In fact, this
result follows immediately from vector field theory once we are told,
in Eq. (176), that the electric field
is the gradient of a scalar potential. The work done on the particle
when it is taken around a closed loop is zero, so
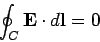 |
(183) |
for any closed loop  . This implies from Stokes' theorem that
. This implies from Stokes' theorem that
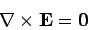 |
(184) |
for any electric field generated by stationary charges. Equation (184)
also follows directly
from Eq. (176), since
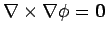 for any scalar potential
for any scalar potential
 .
.
The SI unit of electric potential is the volt, which is equivalent to a joule
per coulomb. Thus, according to Eq. (182),
the electrical work done on a particle when it is
taken between two points is the product of its charge and the voltage difference
between the points.
We are familiar with the idea that a particle moving in
a gravitational field possesses potential energy as well as kinetic
energy. If the particle moves from point  to a lower point
to a lower point  then the
gravitational field does work on the particle causing its kinetic energy to
increase. The increase in kinetic energy of the particle is balanced by an
equal decrease in its potential energy, so that the overall energy of the
particle is a conserved quantity. Therefore, the work done on the particle
as it moves from
then the
gravitational field does work on the particle causing its kinetic energy to
increase. The increase in kinetic energy of the particle is balanced by an
equal decrease in its potential energy, so that the overall energy of the
particle is a conserved quantity. Therefore, the work done on the particle
as it moves from  to
to  is minus the difference in its gravitational
potential energy between points
is minus the difference in its gravitational
potential energy between points  and
and  . Of course, it only makes sense to
talk about gravitational potential energy because the gravitational field
is conservative. Thus, the work done in taking a particle between two
points is path independent, and, therefore, well-defined. This means that the
difference in potential energy of the particle between the beginning and end
points is also
well-defined.
We have already seen that
an electric field generated by stationary charges is a conservative field.
In follows that
we can define an electrical potential energy of a particle moving in such a field.
By analogy with gravitational fields, the work done in taking a particle
from point
. Of course, it only makes sense to
talk about gravitational potential energy because the gravitational field
is conservative. Thus, the work done in taking a particle between two
points is path independent, and, therefore, well-defined. This means that the
difference in potential energy of the particle between the beginning and end
points is also
well-defined.
We have already seen that
an electric field generated by stationary charges is a conservative field.
In follows that
we can define an electrical potential energy of a particle moving in such a field.
By analogy with gravitational fields, the work done in taking a particle
from point  to point
to point  is
equal to minus the difference in potential energy of the particle between
points
is
equal to minus the difference in potential energy of the particle between
points  and
and  . It follows from Eq. (182), that
the potential energy of the particle at a general
point
. It follows from Eq. (182), that
the potential energy of the particle at a general
point  , relative to some reference point
, relative to some reference point  (where the potential energy is set to zero), is given by
(where the potential energy is set to zero), is given by
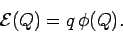 |
(185) |
Free particles try to move down gradients of potential energy, in order to
attain a
minimum potential energy state. Thus, free particles in the Earth's gravitational
field tend to fall downwards.
Likewise, positive charges moving in an electric field
tend to migrate towards regions with the most negative
voltage, and vice versa for negative charges.
The scalar electric potential is undefined to an additive
constant. So, the transformation
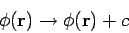 |
(186) |
leaves the electric field unchanged according to Eq. (176).
The potential can be fixed unambiguously
by specifying its value at a single point. The
usual convention is to say that the potential is zero at infinity. This convention
is implicit in Eq. (177), where it can be seen that
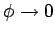 as
as
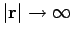 , provided that the total charge
, provided that the total charge
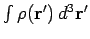 is finite.
is finite.



Next: Gauss' law
Up: Time-independent Maxwell equations
Previous: Coulomb's law
Richard Fitzpatrick
2006-02-02
![\begin{displaymath}
\frac{x - x'}{[(x-x')^2+(y-y')^2 + (z-z')^2]^{ 3/2}}.
\end{displaymath}](img553.png)
![\begin{displaymath}
\frac{x - x'}{[(x-x')^2+(y-y')^2 + (z-z')^2]^{ 3/2}}.
\end{displaymath}](img553.png)
![$\displaystyle \frac{x - x'}{[(x-x')^2+(y-y')^2 + (z-z')^2]^{ 3/2}} = \mbox{\hspace{4cm}}$](img554.png)
![$\displaystyle \mbox{\hspace{4cm}}-\frac{\partial}{\partial x}\!\left(
\frac{1}{[(x-x')^2+(y-y')^2 + (z-z')^2]^{ 1/2}}\right).$](img555.png)
![]() located at the origin is
located at the origin is
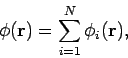
![]() is taken along some path from point
is taken along some path from point ![]() to point
to point ![]() .
The net work done on the particle by electrical forces is
.
The net work done on the particle by electrical forces is
![]() to a lower point
to a lower point ![]() then the
gravitational field does work on the particle causing its kinetic energy to
increase. The increase in kinetic energy of the particle is balanced by an
equal decrease in its potential energy, so that the overall energy of the
particle is a conserved quantity. Therefore, the work done on the particle
as it moves from
then the
gravitational field does work on the particle causing its kinetic energy to
increase. The increase in kinetic energy of the particle is balanced by an
equal decrease in its potential energy, so that the overall energy of the
particle is a conserved quantity. Therefore, the work done on the particle
as it moves from ![]() to
to ![]() is minus the difference in its gravitational
potential energy between points
is minus the difference in its gravitational
potential energy between points ![]() and
and ![]() . Of course, it only makes sense to
talk about gravitational potential energy because the gravitational field
is conservative. Thus, the work done in taking a particle between two
points is path independent, and, therefore, well-defined. This means that the
difference in potential energy of the particle between the beginning and end
points is also
well-defined.
We have already seen that
an electric field generated by stationary charges is a conservative field.
In follows that
we can define an electrical potential energy of a particle moving in such a field.
By analogy with gravitational fields, the work done in taking a particle
from point
. Of course, it only makes sense to
talk about gravitational potential energy because the gravitational field
is conservative. Thus, the work done in taking a particle between two
points is path independent, and, therefore, well-defined. This means that the
difference in potential energy of the particle between the beginning and end
points is also
well-defined.
We have already seen that
an electric field generated by stationary charges is a conservative field.
In follows that
we can define an electrical potential energy of a particle moving in such a field.
By analogy with gravitational fields, the work done in taking a particle
from point ![]() to point
to point ![]() is
equal to minus the difference in potential energy of the particle between
points
is
equal to minus the difference in potential energy of the particle between
points ![]() and
and ![]() . It follows from Eq. (182), that
the potential energy of the particle at a general
point
. It follows from Eq. (182), that
the potential energy of the particle at a general
point ![]() , relative to some reference point
, relative to some reference point ![]() (where the potential energy is set to zero), is given by
(where the potential energy is set to zero), is given by