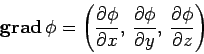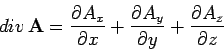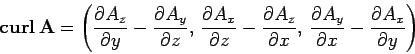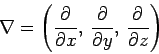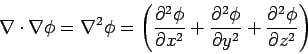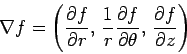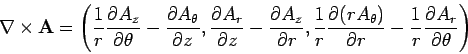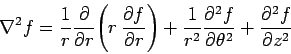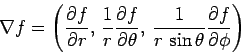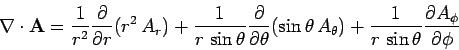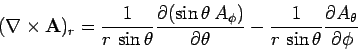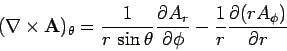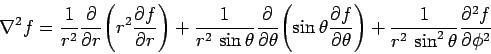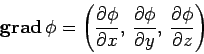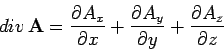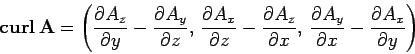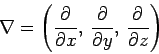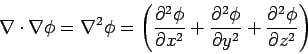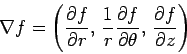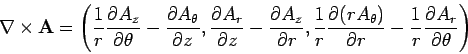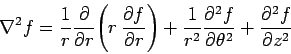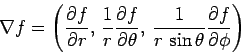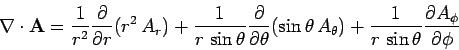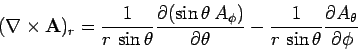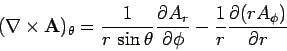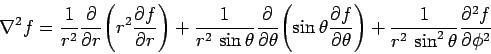

Next: Time-independent Maxwell equations
Up: Vectors
Previous: Curl
- Vector addition:
-
- Vector multiplication:
-
- Scalar product:
-
- Vector product:
-
- Scalar triple product:
-
- Vector triple product:
-
- Gradient:
-
- Divergence:
-
- Curl:
-
- Gauss' theorem:
-
- Stokes' theorem:
-
- Del operator:
-
- Vector identities:
-
- Other vector identities:
-
- Cylindrical polar coordinates:
-
- Spherical polar coordinates:
-


Next: Time-independent Maxwell equations
Up: Vectors
Previous: Curl
Richard Fitzpatrick
2006-02-02