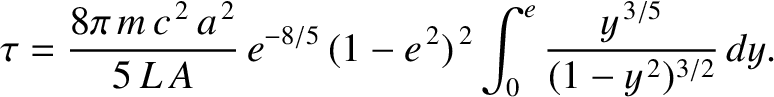Next: Lunar motion Up: Secular perturbation theory Previous: Effect of solar radiation
 ,
,  , and
, and 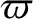 be the orbital major radius, eccentricity, and longitude of the periastron (i.e., the point
of closest approach to the star)
of the first planet, respectively, and let
be the orbital major radius, eccentricity, and longitude of the periastron (i.e., the point
of closest approach to the star)
of the first planet, respectively, and let  ,
, 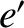 , and
, and 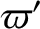 be the the corresponding parameters for the second planet. Suppose that
be the the corresponding parameters for the second planet. Suppose that 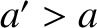 . Let
. Let
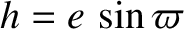 ,
,
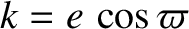 ,
,
 ,
and
,
and
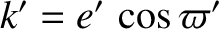 . Consider normal mode solutions of the two planets' secular evolution equations of the form
. Consider normal mode solutions of the two planets' secular evolution equations of the form
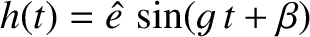 ,
,
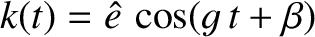 ,
,
 , and
, and
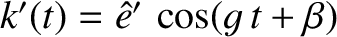 ,
where
,
where
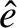 ,
,
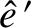 ,
, 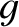 , and
, and 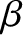 are constants. Demonstrate that
are constants. Demonstrate that
![$\displaystyle \left(\begin{array}{cc}
\skew{3}\hat{g}-q\,\alpha,& q\,\alpha\,\b...
...t{e}'\end{array}\right)=
\left(\begin{array}{c}0\\ [0.5ex]0\end{array}\right),
$](img2866.png)
![$\skew{3}\hat{g}= g/[(1/4)\,\epsilon\,n\,\alpha\,b^{(1)}_{3/2}(\alpha)]$](img2867.png) ,
,
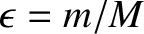 ,
,
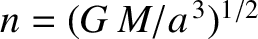 ,
,
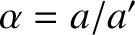 ,
, 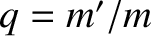 ,
and
,
and
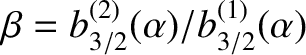 . Here,
. Here,  ,
,  , and
, and  are the masses of the
first planet, second planet, and star, respectively. It is assumed that
are the masses of the
first planet, second planet, and star, respectively. It is assumed that
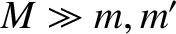 . Hence, deduce that the
general time variation of the osculating orbital elements
. Hence, deduce that the
general time variation of the osculating orbital elements 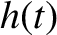 ,
, 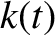 ,
, 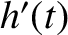 , and
, and 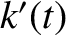 is a linear combination
of two normal modes of oscillation, which are characterized by
is a linear combination
of two normal modes of oscillation, which are characterized by
![$\displaystyle \skew{3}\hat{g} = \frac{1}{2}\left(q\,\alpha+\alpha^{\,3/2}\pm\le...
...,\alpha-\alpha^{\,3/2})^2+4\,q\,\alpha^{5/2}\,\beta^{\,2}\right]^{1/2}\right),
$](img2876.png)

 , in which
, in which
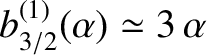 and
and
 , the first normal mode is such that
, the first normal mode is such that
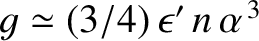 and
and
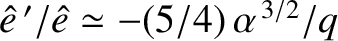 (assuming that
(assuming that
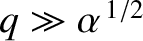 ), whereas the second mode is such that
), whereas the second mode is such that
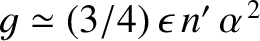 and
and
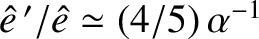 . Here,
. Here,
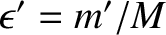 and
and
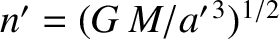 . (Modified
from Murray and Dermott 1999.)
. (Modified
from Murray and Dermott 1999.)

 is the mass of the Sun,
is the mass of the Sun, 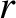 the radial distance of Mercury from the center of the Sun,
the radial distance of Mercury from the center of the Sun, 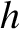 the
conserved angular momentum per unit mass of Mercury, and
the
conserved angular momentum per unit mass of Mercury, and 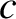 the velocity of light in vacuum. The second
term on the right-hand side of the preceding expression comes from a small general relativistic correction to Newtonian gravity (Rindler 1977). Show that Mercury's equation of motion can be written in the standard form
the velocity of light in vacuum. The second
term on the right-hand side of the preceding expression comes from a small general relativistic correction to Newtonian gravity (Rindler 1977). Show that Mercury's equation of motion can be written in the standard form
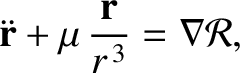
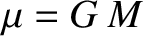 , and
, and
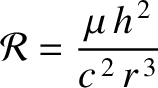
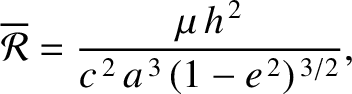
 and
and  are the major radius and eccentricity, respectively, of Mercury's orbit. Hence, deduce from
Lagrange's planetary equations that the general relativistic correction causes the argument of the perihelion of
Mercury's orbit to precess at the rate
are the major radius and eccentricity, respectively, of Mercury's orbit. Hence, deduce from
Lagrange's planetary equations that the general relativistic correction causes the argument of the perihelion of
Mercury's orbit to precess at the rate
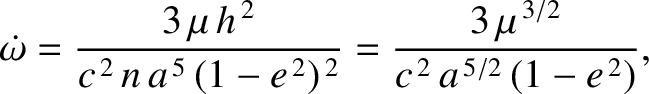
 is Mercury's mean orbital angular velocity.
Finally, show that the preceding expression evaluates to
is Mercury's mean orbital angular velocity.
Finally, show that the preceding expression evaluates to
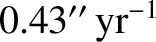 .
.
![$\displaystyle {\mit\Phi}(r,\vartheta) =- \frac{\mu}{r}\left[1-J_2\left(\frac{R}...
...s\vartheta) -
J_3 \left(\frac{R}{r}\right)^3 P_3(\cos\vartheta)+\cdots\right],
$](img2893.png)
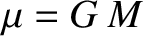 ,
,  is the terrestrial mass,
is the terrestrial mass, 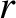 ,
,  ,
, 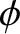 are spherical coordinates that are centered on the Earth, and
aligned with its axis of rotation,
are spherical coordinates that are centered on the Earth, and
aligned with its axis of rotation, 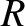 is the Earth's equatorial radius, and
is the Earth's equatorial radius, and
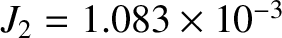 ,
,
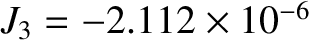 (Yoder 1995). In the preceding expression, the term involving
(Yoder 1995). In the preceding expression, the term involving 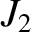 is caused by
the Earth's small oblateness, and the term
involving
is caused by
the Earth's small oblateness, and the term
involving  is caused by the Earth's slightly asymmetric mass distribution between its northern and southern hemispheres. Consider an artificial satellite in orbit around the Earth.
Let
is caused by the Earth's slightly asymmetric mass distribution between its northern and southern hemispheres. Consider an artificial satellite in orbit around the Earth.
Let  ,
,  ,
,  , and
, and 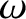 be the orbital major radius, eccentricity, inclination (to the Earth's equatorial plane),
and argument of the perigee, respectively. Furthermore, let
be the orbital major radius, eccentricity, inclination (to the Earth's equatorial plane),
and argument of the perigee, respectively. Furthermore, let
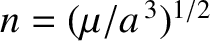 be the unperturbed mean orbital angular velocity.
be the unperturbed mean orbital angular velocity.
Demonstrate that, when averaged over an orbital period, the disturbing function due to the  term
takes the form
term
takes the form
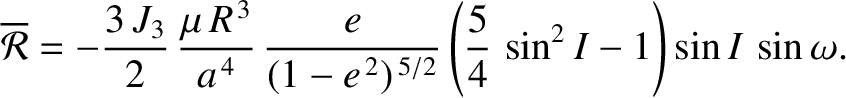
 term causes the eccentricity and inclination of the satellite orbit to evolve in time
as
term causes the eccentricity and inclination of the satellite orbit to evolve in time
as
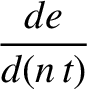 |
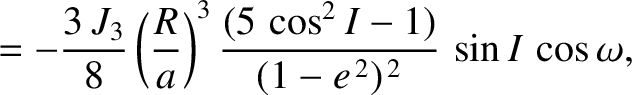 |
|
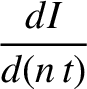 |
 |
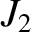 term causes the argument of the perigee to precess at the approximately constant (assuming that the variations in
term causes the argument of the perigee to precess at the approximately constant (assuming that the variations in  and
and  are small) rate
are small) rate
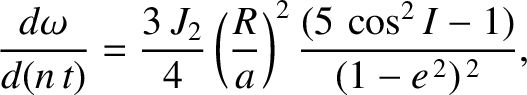
 term can be written
term can be written
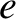 |
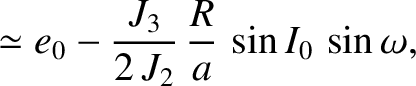 |
|
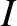 |
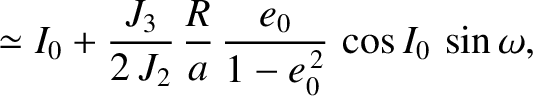 |
 and
and 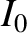 are constants. (Modified from Murray and Dermott 1999.)
are constants. (Modified from Murray and Dermott 1999.)
 executing a Keplerian orbit of major radius
executing a Keplerian orbit of major radius  about an object of mass
about an object of mass  (in a frame of reference in which the latter object is
stationary) are
(in a frame of reference in which the latter object is
stationary) are


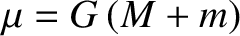 .
.
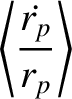 |
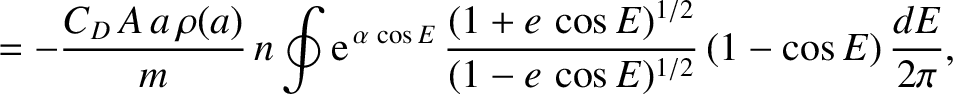 |
|
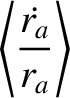 |
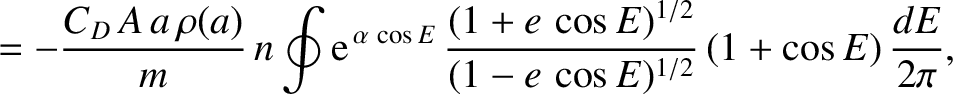 |
 , in which the difference between the apogee and perigee distances is much greater than the
scale height of the atmosphere, the previous expressions reduce to
, in which the difference between the apogee and perigee distances is much greater than the
scale height of the atmosphere, the previous expressions reduce to
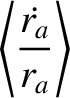 |
 |
|
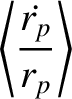 |
 |
 around the Earth. Assume that the altitude,
around the Earth. Assume that the altitude, 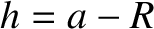 , of the orbit is much less that the
terrestrial radius,
, of the orbit is much less that the
terrestrial radius, 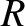 . Using the notation of Section 10.6, show that the time,
. Using the notation of Section 10.6, show that the time, 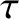 , for the orbit to decay from an initial
altitude
, for the orbit to decay from an initial
altitude 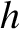 to zero altitude is
to zero altitude is
![$\displaystyle \frac{\tau}{T} = \frac{m}{C_D\,2\pi\,R\,A\,\rho_0}\,\frac{H}{R}\left[\exp\left(\frac{h}{H}\right)-1\right],
$](img2919.png)
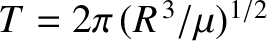 .
.
 , and eccentricity,
, and eccentricity,  , under the action of solar radiation pressure is such that
, under the action of solar radiation pressure is such that

 is a constant. Hence, deduce that the time required for a dust grain in an orbit of initial major
radius
is a constant. Hence, deduce that the time required for a dust grain in an orbit of initial major
radius  and initial eccentricity
and initial eccentricity  to spiral into the Sun is
to spiral into the Sun is