Next: Moment of inertia tensor Up: Rigid body rotation Previous: Introduction
 elements, and let the
elements, and let the 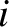 th element be of mass
th element be of mass 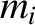 , and instantaneous position
vector
, and instantaneous position
vector 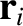 . The equation of motion of the
. The equation of motion of the 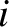 th element
is written
Here,
th element
is written
Here,
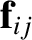 is the internal force exerted on the
is the internal force exerted on the 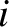 th element by the
th element by the
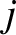 th element, and
th element, and  the external force acting on the
the external force acting on the 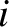 th
element. The internal forces
th
element. The internal forces
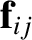 represent the
stresses that develop within the body in order to ensure that its various
elements maintain a fixed spatial relationship with respect to one another.
Of course,
represent the
stresses that develop within the body in order to ensure that its various
elements maintain a fixed spatial relationship with respect to one another.
Of course,
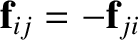 , by Newton's third law.
The external forces represent forces that originate outside the body.
, by Newton's third law.
The external forces represent forces that originate outside the body.
Repeating the analysis of Section 2.6, we can sum Equation (8.1) over all mass elements to obtain
Here,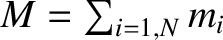 is the total mass,
is the total mass,
 the position vector of the center of mass [see Equation (2.27)],
and
the position vector of the center of mass [see Equation (2.27)],
and
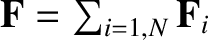 the total external force.
It can be seen that the center of mass of a rigid body moves under the action of the external forces like
a point particle whose mass is identical with that of the body.
the total external force.
It can be seen that the center of mass of a rigid body moves under the action of the external forces like
a point particle whose mass is identical with that of the body.
Again repeating the analysis of Section 2.6, we can sum
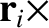 Equation (8.1) over all mass elements to obtain
Equation (8.1) over all mass elements to obtain
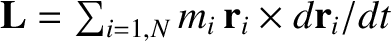 is the
total angular momentum of the body (about the origin), and
is the
total angular momentum of the body (about the origin), and
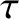
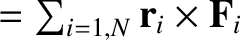 the
total external torque (about the origin). The preceding equation is
only valid if the internal forces are central in nature. However, this
is not a particularly onerous constraint. Equation (8.3) describes
how the angular momentum of a rigid body evolves in time under the action
of
the external torques.
the
total external torque (about the origin). The preceding equation is
only valid if the internal forces are central in nature. However, this
is not a particularly onerous constraint. Equation (8.3) describes
how the angular momentum of a rigid body evolves in time under the action
of
the external torques.
In the following, we shall only consider the rotational motion of rigid bodies, because their translational motion is similar to that of point particles [see Equation (8.2)] and, therefore, is fairly straightforward in nature.